РОС, ответы на задачи
Материал из eSyr's wiki.
(→Задача 6 (Алгоритм задиры)) |
(→Задача 5 (суммирование)) |
||
| (30 промежуточных версий не показаны.) | |||
| Строка 12: | Строка 12: | ||
Видимо, при отсутствии таких механизмов, необходимо воспользоваться паравиртуализацией (эмуляция аппаратных средств + гипервизор (ОС)). | Видимо, при отсутствии таких механизмов, необходимо воспользоваться паравиртуализацией (эмуляция аппаратных средств + гипервизор (ОС)). | ||
| - | Защита памяти --- защита оперативной памяти. Привилегированный режим необходим для защиты внешней памяти. | + | Защита памяти --- защита оперативной памяти. Привилегированный режим необходим для защиты внешней памяти (''SkyHawk:'' Неправда, привилегированный режим необходим для реализации защиты памяти, иначе любой процесс сможет делать то же, что и ОС, а именно влезать в чужую память.). |
== Тема 2 == | == Тема 2 == | ||
| Строка 48: | Строка 48: | ||
Имеется механизм двоичных семафоров. Опираясь на него, реализуйте P-операцию и V-операцию для общего (считающего) семафора. | Имеется механизм двоичных семафоров. Опираясь на него, реализуйте P-операцию и V-операцию для общего (считающего) семафора. | ||
| - | '''Ответ | + | '''Ответ (не реализовано "блокирование" в случае если процесс ждет входа, заменено циклом)''' |
<pre> | <pre> | ||
| - | + | int count = N; | |
| - | + | boolSemaphore sem = 1; | |
| - | + | ||
| - | + | P(s) { | |
| - | + | bool success = false; | |
| - | + | while(!success) { | |
| - | + | P(sem); | |
| - | + | if(count > 0) {count--; success = true;} | |
| - | + | V(sem); | |
| - | + | } | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
} | } | ||
| - | + | ||
| - | + | V(s) { | |
| - | + | P(sem); | |
| - | + | count++; | |
| - | + | V(sem); | |
| - | + | ||
| - | + | ||
} | } | ||
</pre> | </pre> | ||
| Строка 92: | Строка 75: | ||
Semaphore wait = 1; // при помощи него мы будет реализовывать ожидание. | Semaphore wait = 1; // при помощи него мы будет реализовывать ожидание. | ||
| - | P(S) { | + | P(Int S) { |
| - | P( | + | wait.P(); |
| - | P( | + | access.P(); |
S = S – 1; | S = S – 1; | ||
| - | If(S > 0) V( | + | If(S > 0) wait.V(); //если мы последним вошли в критическую секцию(S == 0) - залочили после себя всех |
| - | V( | + | access.V(); |
} | } | ||
| - | V(S) { | + | V(Int S) { |
| - | P( | + | access.P(); |
S++; | S++; | ||
| - | If(S == 1) V( | + | If(S == 1) wait.V(); //мы освобождаем единственное место - надо разлочить ожидающих, если мы освобождаем второе и далее место - значит очереди нет, никого разлочивать не надо |
| - | V( | + | access.V(); |
} | } | ||
</pre> | </pre> | ||
| - | |||
=== Задача 3 (события через двоичный семафор) === | === Задача 3 (события через двоичный семафор) === | ||
| Строка 166: | Строка 148: | ||
float A[ L1 ][ L2 ]; | float A[ L1 ][ L2 ]; | ||
| - | struct | + | struct event s[ L1 ][ L2 ]; |
for ( i = 0; i < L1; i++) // Цикл 1 | for ( i = 0; i < L1; i++) // Цикл 1 | ||
| Строка 195: | Строка 177: | ||
for ( j = 1; j < L2-1; j++) | for ( j = 1; j < L2-1; j++) | ||
A[ i ][ j ] = (A[ i-1 ][ j ] + A[ i+1 ][ j ] + A[ i ][ j-1 ] + A[ i ][ j+1 ]) / 4; | A[ i ][ j ] = (A[ i-1 ][ j ] + A[ i+1 ][ j ] + A[ i ][ j-1 ] + A[ i ][ j+1 ]) / 4; | ||
| + | |||
| + | <s>Нет, события использованы неправильно, так как забыли назначить посчитанным первый столбец: | ||
| + | |||
| + | for ( i = 0; i < L1; i++) // Это надо вставить до начала | ||
| + | post( s[ i ][ 0 ]) // основного цикла | ||
| + | |||
| + | Т.е. конечный вариант: | ||
| + | </s> | ||
| + | |||
| + | Нет, это не нужно, потому что этих событий никто никогда не ждет! Это нужно только для варианта алгоритма с двумя parfor (по i и по j) – в нем есть еще один wait. | ||
| + | Так что события здесь использованы корректно, но для такого варианта достаточно и семафоров. | ||
| + | <s> | ||
| + | <pre> | ||
| + | float A[ L1 ][ L2 ]; | ||
| + | struct event s[ L1 ][ L2 ]; | ||
| + | for ( i = 0; i < L1; i++) // Цикл 1 | ||
| + | for ( j = 0; j < L2; j++) | ||
| + | { clear( s[ i ][ j ]) } | ||
| - | + | for ( j = 0; j < L2; j++) // Цикл 2 | |
| + | { post( s[ 0 ][ j ]) } | ||
| + | |||
| + | for ( i = 0; i < L1; i++) | ||
| + | { post( s[ i ][ 0 ]) } | ||
| + | |||
| + | parfor ( i = 1; i < L1-1; i++) // Цикл 3 | ||
| + | for ( j = 1; j < L2-1; j++) | ||
| + | { | ||
| + | wait( s[ i-1 ][ j ]); | ||
| + | A[ i ][ j ] = (A[ i-1 ][ j ] + A[ i+1 ][ j ] + A[ i ][ j-1 ] + A[ i ][ j+1 ]) / 4; | ||
| + | post( s[ i ][ j ]); | ||
| + | } | ||
| + | </pre> | ||
| + | </s> | ||
| + | Причем, wait( s[ i ][ j-1 ]); делать во внутреннем цикле "Цикл 3" не нужно, так как внутри мы имеем for, а не parfor - это отличие данного алгоритма от алгоритма в лекциях. | ||
<u>Оценка времени выполнения</u>: | <u>Оценка времени выполнения</u>: | ||
| Строка 205: | Строка 220: | ||
** каждый процессор (кроме последнего) получает для обработки <math>\lceil (L1-2) / N \rceil </math> строк. | ** каждый процессор (кроме последнего) получает для обработки <math>\lceil (L1-2) / N \rceil </math> строк. | ||
** пока первая нить обрабатывает все свои строки, кроме своей последней, все остальные нити простаивают. Преимущество возникает, когда первая нить начинает обрабатывать свою последнюю строку. После того, как первая нить подсчитает первый элемент этой строки, в работу включится вторая нить, и L2-3 элемента первая и вторая нить будут обрабатывать параллельно. Далее первая нить будет простаивать, а работать будет вторая нить. | ** пока первая нить обрабатывает все свои строки, кроме своей последней, все остальные нити простаивают. Преимущество возникает, когда первая нить начинает обрабатывать свою последнюю строку. После того, как первая нить подсчитает первый элемент этой строки, в работу включится вторая нить, и L2-3 элемента первая и вторая нить будут обрабатывать параллельно. Далее первая нить будет простаивать, а работать будет вторая нить. | ||
| - | ** как можно видеть, преимущество возникает только на таких таких строках m, что: m-я строка распределена k-й нити, а строка m+1 - нити с номером k+1. В каждом таком случае мы получаем преимущество по времени равное <math>(L2-3)</math>. Всего таких номеров m ровно N-1. | + | ** как можно видеть, преимущество возникает только на таких таких строках m, что: m-я строка распределена k-й нити, а строка m+1 - нити с номером k+1. В каждом таком случае мы получаем преимущество по времени равное <math>(L2-3)</math>. Всего таких номеров m ровно N-1. Суммарный выигрыш получается равным <math>(N-1)*(L2-3)</math> |
| - | ** итого, время параллельного выполнения составляет ''' <math>(L1-2) * (L2-2) - N*(L2-3) </math>''' | + | ** итого, время параллельного выполнения составляет ''' <math>(L1-2) * (L2-2) - (N-1)*(L2-3) </math>''' |
| + | |||
| + | === Задача 6 (Писатели и читатели) === | ||
| + | Имеется механизм двоичных семафоров. Опираясь на него, реализуйте задачу читателей и писателей (алгоритмы предоставления прав доступа процессам-читателям и процессам-писателям): | ||
| + | |||
| + | ''Процесс-писатель должен получать исключительный (монопольный) доступ к базе данных (других писателей или каких-либо читателей быть не должно). Произвольное число процессов-читателей может работать одновременно, но любой читатель может получить доступ только при отсутствии работающих писателей. '' | ||
| + | |||
| + | Запросы на доступ должны удовлетворяться “справедливо” - в порядке их поступления (можно исходить из “справедливости“ удовлетворения запросов на двоичные семафоры). | ||
| + | |||
| + | '''Ответ:''' | ||
| + | |||
| + | <pre> | ||
| + | semaphore sem_r = 1, sem_ra = 1, sem_w = 1; | ||
| + | int readers_count = 0; | ||
| + | |||
| + | r_enter() { // Читатель хочет начать читать | ||
| + | sem_r.P(); | ||
| + | sem_ra.P(); | ||
| + | ++readers_count; | ||
| + | if (readers_count == 1) | ||
| + | sem_w.P(); // Первый читатель блокирует возможность писать | ||
| + | sem_ra.V(); | ||
| + | sem_r.V(); | ||
| + | } | ||
| + | |||
| + | r_leave() { // Читатель выходит из области чтения | ||
| + | sem_ra.P(); | ||
| + | --readers_count; | ||
| + | if (readers_count == 0) | ||
| + | sem_w.V(); // Последний читатель освобождает семафор | ||
| + | sem_ra.V(); | ||
| + | } | ||
| + | |||
| + | w_enter() { // Писатель хочет писать | ||
| + | sem_r.P(); // Чтобы новые читатели не начинали читать и чтобы | ||
| + | // избежать блокировки при одновременном входе читателя и писателя. | ||
| + | sem_w.P(); | ||
| + | } | ||
| + | |||
| + | w_leave() { // Писатель выходит из области записи | ||
| + | sem_w.V(); | ||
| + | sem_r.V(); | ||
| + | } | ||
| + | |||
| + | </pre> | ||
== Тема 3 == | == Тема 3 == | ||
| Строка 263: | Строка 322: | ||
'''Ответ:''' | '''Ответ:''' | ||
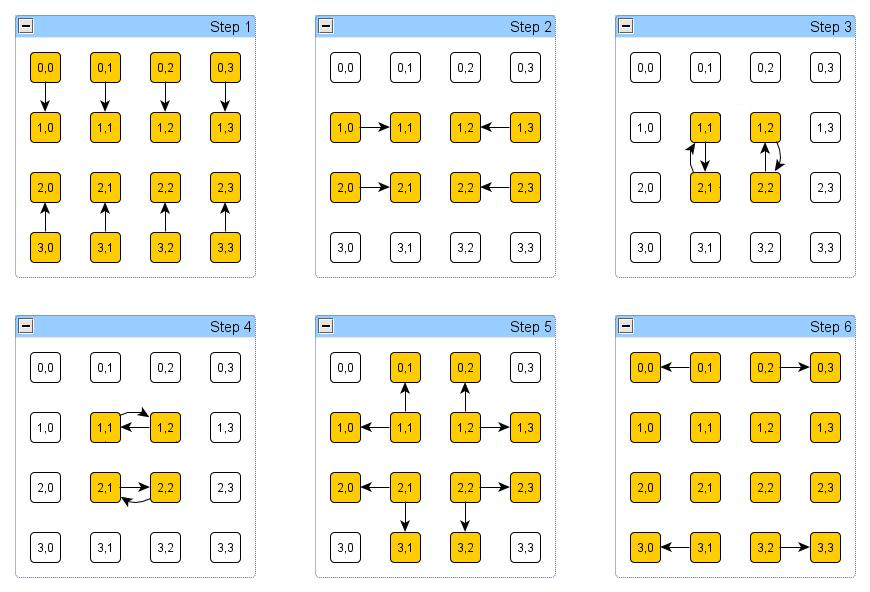
| - | Пусть никакой буферизации не предусмотрено. Для получения суммы на одном из четырёх центральных процессов ((1,1),(2,1),(1,2),(2,2)) необходимо 4 операции (2 операции для получения суммы своего угла из 4 процессов для каждого центрального процесса, ещё две, чтобы получить общую сумму на всех - на каждом такте складываем сумму на транспьтере с соседями (к примеру, (1,1) с (2,1) и (1, 2). После этого на каждом из 4х транспьютеров получается удвоенная сумма, из которой получается просто сумма)). Затем нужно ещё 2 операции, чтобы разослать информацию во все углы. Итого: 6*(Ts+Tb). | + | Пусть никакой буферизации не предусмотрено. Для получения суммы на одном из четырёх центральных процессов ((1,1),(2,1),(1,2),(2,2)) необходимо 4 операции (2 операции для получения суммы своего угла из 4 процессов для каждого центрального процесса, ещё две, чтобы получить общую сумму на всех - <s>на каждом такте складываем сумму на транспьтере с соседями (к примеру, (1,1) с (2,1) и (1, 2). После этого на каждом из 4х транспьютеров получается удвоенная сумма, из которой получается просто сумма)</s> Неправильно, при таких операциях получатся числа вида 3a+2b+2c+2d, 2a+3b+2c+2d и т. п.. На самом деле нужно на первом такте (3) переслать числа по вертикали (от (2,1) к (3,1) и обратно, от (2,2) к (3,2) и обратно, при этом каждый прибавляет полученное значение к своему, так получатся a+c, c+a и b+d, d+b. На втором такте (4) – аналогично по горизонтали, получится полная сумма во всех четырех вершинах). Затем нужно ещё 2 операции, чтобы разослать информацию во все углы. Итого: 6*(Ts+Tb). |
| - | [[Изображение:4x4sum. | + | [[Изображение:4x4sum.png]] |
Если процессов 64, то разобьём квадрат на 4 подквадрата. Как было показано ранее, за 4 операции пожно получить сумму своего квадрата в (2,2), (5,2), (2,5) и (5,5). Ещё две операции нужно на пересылку в центральные процессы. Там за 2 операции получаем сумму на всех из них (как и в первом случае), и ещё 6 на рассылку. Итого: 14*(Ts+Tb). | Если процессов 64, то разобьём квадрат на 4 подквадрата. Как было показано ранее, за 4 операции пожно получить сумму своего квадрата в (2,2), (5,2), (2,5) и (5,5). Ещё две операции нужно на пересылку в центральные процессы. Там за 2 операции получаем сумму на всех из них (как и в первом случае), и ещё 6 на рассылку. Итого: 14*(Ts+Tb). | ||
| Строка 279: | Строка 338: | ||
=== Задача 7 (передача сообщения) === | === Задача 7 (передача сообщения) === | ||
| - | В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо переслать очень длинное сообщение (длиной L байт) из узла с координатами (0,0) в узел с координатами (3,3) | + | В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо переслать очень длинное сообщение (длиной L байт) из узла с координатами (0,0) в узел с координатами (3,3). Сколько времени потребуется для этого? А сколько времени потребуется для пересылки из узла с координатами (1,1) в узел с координатами (2,2)? Время старта равно времени передачи байта (Ts=Tb). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми. |
'''Ответ:''' | '''Ответ:''' | ||
| Строка 288: | Строка 347: | ||
: max{ 2*(Ts+Tb*N/(2K1))+(K1-1)*(Ts+Tb*N/(2K1)), 6*(Ts+Tb*(L-N)/(2K2))+(K2-1)*(Ts+Tb*(L-N)/(2K2)) }. | : max{ 2*(Ts+Tb*N/(2K1))+(K1-1)*(Ts+Tb*N/(2K1)), 6*(Ts+Tb*(L-N)/(2K2))+(K2-1)*(Ts+Tb*(L-N)/(2K2)) }. | ||
И эту жесть надо минимизировать по N, K1, K2. | И эту жесть надо минимизировать по N, K1, K2. | ||
| + | |||
| + | '''Ответ (вариант 2):''' | ||
| + | |||
| + | На консультации сказали, что если в задании есть слова ''очень длинное сообщение'', то можно пренебречь временем старта, временем разгона конвейера и длиной маршрута. Таким образом, у нас остается только Tb. Тогда из (0,0) в (3,3) можно переслать сообщение за время L*Tb/2 (т. к. возможно два маршрута), из (1,1) в (2,2) -- за время L*Tb/4 (т. к. в этом случае 4 маршрута). | ||
=== Задача 8 (буферизуемая передача сообщения) === | === Задача 8 (буферизуемая передача сообщения) === | ||
| Строка 326: | Строка 389: | ||
Замечание: в приведенном выше решении, на мой взгляд, имеется ошибка - не учтены повторные посылки запроса после того, как маркер покидает вершину, в направлении ушедшего маркера (они выполняются, если очередь запросов в узле не пуста). Их количество считается вручную (мысленно проводим обход дерева и при каждом переходе в следующую вершину смотрим, остались ли еще запросы на только что покинутой). На приведенном выше рисунке, таким образом, строя обход в глубину справа налево, нужно к ответу добавить 11*(Ts+1*Tb). Данное решение принято аспирантом на экзамене, кроме того, им было сделано замечание, что запрос может посылаться вместе с маркером в одном сообщении, тогда удастся избежать лишних накладных расходов на инициацию передачи и к ответу добавится просто 11*Tb. | Замечание: в приведенном выше решении, на мой взгляд, имеется ошибка - не учтены повторные посылки запроса после того, как маркер покидает вершину, в направлении ушедшего маркера (они выполняются, если очередь запросов в узле не пуста). Их количество считается вручную (мысленно проводим обход дерева и при каждом переходе в следующую вершину смотрим, остались ли еще запросы на только что покинутой). На приведенном выше рисунке, таким образом, строя обход в глубину справа налево, нужно к ответу добавить 11*(Ts+1*Tb). Данное решение принято аспирантом на экзамене, кроме того, им было сделано замечание, что запрос может посылаться вместе с маркером в одном сообщении, тогда удастся избежать лишних накладных расходов на инициацию передачи и к ответу добавится просто 11*Tb. | ||
| + | |||
| + | Замечание2: А если начать обход не с 0 вершины, а с 15? тогда нам потребуется только 23 операции (т.к не придется дважды проходить 15-13, 13-9, 9-0) | ||
===Задача 3 (Децентрализованный алгоритм с временными метками)=== | ===Задача 3 (Децентрализованный алгоритм с временными метками)=== | ||
| Строка 346: | Строка 411: | ||
'''Ответ:''' | '''Ответ:''' | ||
| - | Маркер находится у процесса 0. Он спокойно входит в КС, а все остальные шлют broadcast запросы о | + | Маркер находится у процесса 0. Он спокойно входит в КС, а все остальные шлют broadcast запросы о желании войти в КС. Им нужно для этого 15*16 тактов, так как нет аппаратной поддержки широковещания. После этого у маркера сформировалась очередь из 15 желающих войти в КС, и он по очереди удовлетворяет их желания (на каждое нужна одна пересылка маркера). Всего получается 15*16+15 тактов. Можно чередовать операции рассылки и передачи маркера, но их всё равно будет столько же. Ответ: 15*16*(Ts+Tb*Lreq) + 15*(Ts+Tb*Lmark). |
Заметьте, что здесь Lmark довольно большая. В сообщение должны помещаться очередь длины 1..15 и массив из 16 номеров последних запросов. | Заметьте, что здесь Lmark довольно большая. В сообщение должны помещаться очередь длины 1..15 и массив из 16 номеров последних запросов. | ||
| Строка 534: | Строка 599: | ||
Консистентность памяти по входу и алгоритм ее реализации в DSM с полным размножением. Сколько времени потребует трехкратное выполнение критической секции и модификация в ней 11 переменных каждым процессом, если DSM реализована на 10 ЭВМ сети с шинной организацией(с аппаратными возможностями широковещания). Время старта (время разгона после получения доступа к шине для передачи) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми. | Консистентность памяти по входу и алгоритм ее реализации в DSM с полным размножением. Сколько времени потребует трехкратное выполнение критической секции и модификация в ней 11 переменных каждым процессом, если DSM реализована на 10 ЭВМ сети с шинной организацией(с аппаратными возможностями широковещания). Время старта (время разгона после получения доступа к шине для передачи) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми. | ||
| + | ''Примечание: решение не верное, лектор сказал надо использовать какой-нибудь алгоритм с маркером.'' <br> | ||
'''Ответ:''' Консистентность памяти по входу (она же поэлементная в Таненбауме), закрепляет каждую разделяемую переменную за своей синхронизационной переменной. Поэтому для изменения каждой переменной необходимо производить свой захват и освобождение синхронизационной переменной. Так как Крюков сказал, что нужны децентрализованные алгоритмы, пользуемся таким. | '''Ответ:''' Консистентность памяти по входу (она же поэлементная в Таненбауме), закрепляет каждую разделяемую переменную за своей синхронизационной переменной. Поэтому для изменения каждой переменной необходимо производить свой захват и освобождение синхронизационной переменной. Так как Крюков сказал, что нужны децентрализованные алгоритмы, пользуемся таким. | ||
| Строка 561: | Строка 627: | ||
Сначала прогоняем синхронную фиксацию консистентного множества КТ. Это потребует T1. Эти контрольные точки будем считать промежуточными. | Сначала прогоняем синхронную фиксацию консистентного множества КТ. Это потребует T1. Эти контрольные точки будем считать промежуточными. | ||
| - | + | Исходя из определения, для того, чтобы консистентное множество точек стало строго консистентным, надо убедиться, что между процессами нет никаких сообщений. Для этого мы можем просто пропустить по всем каналам свои собственные сообщения. Если они все пройдут, значит, каналы пусты и множество строго консистентно. Однако, стоит обратить внимание, что координатор уже посылал всем служебные сообщения, так что его каналы проверять не нужно. У нас остается 11 ЭВМ, которые хотят проверить по 10 каналов каждая. ЭВМ запоминают, по каким каналам им приходят эти служебные сообщения. Если придут по всем 10, посылают сообщение координатору с указанием того, что они готовы к созданию точки. Если координатору придут все сообщения, он рассылает уведомление о фиксации множества. | |
| + | |||
| + | ''Примечание: n(n-1) - плохая оценка, надо не проверять все каналы, а просто считать отосланные сообщения'' | ||
Итак, по полочкам: | Итак, по полочкам: | ||
Текущая версия
[править] Тема 1
1. Какие аппаратные механизмы необходимы для организации мультипрограммного режима? Как обеспечить мультипрограммный режим без этих механизмов? Как обеспечить, если отсутствует только один из них?
Ответ:
Для реализации мультипрограммного режима необходимы:
- Поддержка различных режимов выполнения (привилегированный и непривилегированный режим).
- Поддержка механизма защиты памяти (каждый процесс выполняется в своем адресном пространстве).
- Поддержка механизма прерываний (сигнализировать ОС об истечении кванта времени, сигнализировать о том, что процесс полез не в свою память).
- Поддержка таймера (кванты времени).
Видимо, при отсутствии таких механизмов, необходимо воспользоваться паравиртуализацией (эмуляция аппаратных средств + гипервизор (ОС)).
Защита памяти --- защита оперативной памяти. Привилегированный режим необходим для защиты внешней памяти (SkyHawk: Неправда, привилегированный режим необходим для реализации защиты памяти, иначе любой процесс сможет делать то же, что и ОС, а именно влезать в чужую память.).
[править] Тема 2
[править] Задача 1 (Деккер)
Если в алгоритме Деккера (enwiki) не изменять значение переменной turn при выходе из критической секции, то каким требованиям он перестанет удовлетворять? Объясните, почему.
flag[0] := false
flag[1] := false
turn := 0 // or 1
p0: p1:
flag[0] := true flag[1] := true
while flag[1]=true { while flag[0]=true {
if turn ≠ 0 { if turn ≠ 1 {
flag[0] := false flag[1] := false
while turn ≠ 0 { while turn ≠ 1 {
} }
flag[0] := true flag[1] := true
} }
} }
// critical section // critical section
... ...
// remainder section // remainder section
turn := 1 turn := 0
flag[0] := false flag[1] := false
Ответ:
Требованию конечного ожидания входа в критическую секцию --- после такой модификации один из процессов будет бесконечно долго ждать входа в критическую секцию (starvation).
[править] Задача 2 (считающий семафор через двоичный)
Имеется механизм двоичных семафоров. Опираясь на него, реализуйте P-операцию и V-операцию для общего (считающего) семафора.
Ответ (не реализовано "блокирование" в случае если процесс ждет входа, заменено циклом)
int count = N;
boolSemaphore sem = 1;
P(s) {
bool success = false;
while(!success) {
P(sem);
if(count > 0) {count--; success = true;}
V(sem);
}
}
V(s) {
P(sem);
count++;
V(sem);
}
Ответ (2 вариант, из лекций)
Int S = N;
Semaphore access = 1; // семафор для монопольного доступа к S
Semaphore wait = 1; // при помощи него мы будет реализовывать ожидание.
P(Int S) {
wait.P();
access.P();
S = S – 1;
If(S > 0) wait.V(); //если мы последним вошли в критическую секцию(S == 0) - залочили после себя всех
access.V();
}
V(Int S) {
access.P();
S++;
If(S == 1) wait.V(); //мы освобождаем единственное место - надо разлочить ожидающих, если мы освобождаем второе и далее место - значит очереди нет, никого разлочивать не надо
access.V();
}
[править] Задача 3 (события через двоичный семафор)
Имеется механизм двоичных семафоров. Опираясь на него, реализуйте операторы POST(имя переменной-события) и WAIT(имя переменной-события).
Ответ:
BinarySemaphore sem; // семафор должен быть в захваченном состоянии.
void event::POST() {
sem.V();
}
void event::WAIT() {
sem.P();
sem.V();
}
[править] Задача 4 (двоичный семафор через TSL/прерывания)
Имеется команда TSL и команда объявления прерывания указанному процессору. Опираясь на него, реализуйте на мультипроцессоре P-операцию и V-операцию для двоичного семафора. Активное ожидание освобождения семафора не допускается.
Ответ:
Чтобы не заморачиваться на регистровый вариант TSL можно предложить его логический аналог
bool tsl(bool& val){
bool i = val;
val = 1;
return i;
}
val = 0 // пусть это означает, что семафор свободен
void P(){
r = tsl(val) // получили старое значение val и поменяли его
if(r){
<добавляем себя в список ждущих>
<ждем прерывания>
<удаляем себя из списка ждущих>
}
}
void V(){
if(<список ждущих не пуст>){
<шлем прерывание 1 из списка>
}
else{val = 0}
}
Ответ(вариант 2):
Tsl(r, s) делает [r = s, s = 1] – это неделимая операция.
[править] Задача 5 (верхняя релаксация)
Правильно ли использованы события в алгоритме, который реализует метод верхней релаксации? Оцените, насколько этот алгоритм можно выполнить быстрее, чем последовательный, если число процессоров мультипроцессора = N, время выполнения одного оператора присваивания (A[i][j]=....) равно 1, временами выполнения остальных операторов можно пренебречь.
float A[ L1 ][ L2 ];
struct event s[ L1 ][ L2 ];
for ( i = 0; i < L1; i++) // Цикл 1
for ( j = 0; j < L2; j++)
{ clear( s[ i ][ j ]) }
for ( j = 0; j < L2; j++) // Цикл 2
{ post( s[ 0 ][ j ]) }
parfor ( i = 1; i < L1-1; i++) // Цикл 3
for ( j = 1; j < L2-1; j++)
{
wait( s[ i-1 ][ j ]);
A[ i ][ j ] = (A[ i-1 ][ j ] + A[ i+1 ][ j ] + A[ i ][ j-1 ] + A[ i ][ j+1 ]) / 4;
post( s[ i ][ j ]);
}
Ответ: Введу читателя в курс дела:
- Механизм событий
- POST(S) – объявление события S (является аналогом "V(S);" - освобождение семаформа S)
- WAIT(S) – процесс ожидает, когда произойдет событие S (является аналогом "P(S);V(S);" - освобождение семаформа S)
- CLEAR(S) – чистим значение S (я полагаю, эквивалентно S := 0, если продолжать аналогию с семаформа)
- Parfor - это цикл, витки которого распределяются между нитями (или процессами).
- Алгоритм последовательной верхней релаксации выглядит так:
for ( i = 1; i < L1-1; i++)
for ( j = 1; j < L2-1; j++)
A[ i ][ j ] = (A[ i-1 ][ j ] + A[ i+1 ][ j ] + A[ i ][ j-1 ] + A[ i ][ j+1 ]) / 4;
Нет, события использованы неправильно, так как забыли назначить посчитанным первый столбец:
for ( i = 0; i < L1; i++) // Это надо вставить до начала
post( s[ i ][ 0 ]) // основного цикла
Т.е. конечный вариант:
Нет, это не нужно, потому что этих событий никто никогда не ждет! Это нужно только для варианта алгоритма с двумя parfor (по i и по j) – в нем есть еще один wait.
Так что события здесь использованы корректно, но для такого варианта достаточно и семафоров.
float A[ L1 ][ L2 ];
struct event s[ L1 ][ L2 ];
for ( i = 0; i < L1; i++) // Цикл 1
for ( j = 0; j < L2; j++)
{ clear( s[ i ][ j ]) }
for ( j = 0; j < L2; j++) // Цикл 2
{ post( s[ 0 ][ j ]) }
for ( i = 0; i < L1; i++)
{ post( s[ i ][ 0 ]) }
parfor ( i = 1; i < L1-1; i++) // Цикл 3
for ( j = 1; j < L2-1; j++)
{
wait( s[ i-1 ][ j ]);
A[ i ][ j ] = (A[ i-1 ][ j ] + A[ i+1 ][ j ] + A[ i ][ j-1 ] + A[ i ][ j+1 ]) / 4;
post( s[ i ][ j ]);
}
Причем, wait( s[ i ][ j-1 ]); делать во внутреннем цикле "Цикл 3" не нужно, так как внутри мы имеем for, а не parfor - это отличие данного алгоритма от алгоритма в лекциях.
Оценка времени выполнения:
- Остановимся на оценке времени выполнения Цикла 3.
- Последовательное выполнение (без операторов wait и post) требует (L1 − 2) * (L2 − 2) присваиваний.
- При работе на N процессорах (без учета операторов wait и post):
- каждый процессор (кроме последнего) получает для обработки
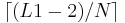 строк.
строк.
- пока первая нить обрабатывает все свои строки, кроме своей последней, все остальные нити простаивают. Преимущество возникает, когда первая нить начинает обрабатывать свою последнюю строку. После того, как первая нить подсчитает первый элемент этой строки, в работу включится вторая нить, и L2-3 элемента первая и вторая нить будут обрабатывать параллельно. Далее первая нить будет простаивать, а работать будет вторая нить.
- как можно видеть, преимущество возникает только на таких таких строках m, что: m-я строка распределена k-й нити, а строка m+1 - нити с номером k+1. В каждом таком случае мы получаем преимущество по времени равное (L2 − 3). Всего таких номеров m ровно N-1. Суммарный выигрыш получается равным (N − 1) * (L2 − 3)
- итого, время параллельного выполнения составляет (L1 − 2) * (L2 − 2) − (N − 1) * (L2 − 3)
- каждый процессор (кроме последнего) получает для обработки
[править] Задача 6 (Писатели и читатели)
Имеется механизм двоичных семафоров. Опираясь на него, реализуйте задачу читателей и писателей (алгоритмы предоставления прав доступа процессам-читателям и процессам-писателям):
Процесс-писатель должен получать исключительный (монопольный) доступ к базе данных (других писателей или каких-либо читателей быть не должно). Произвольное число процессов-читателей может работать одновременно, но любой читатель может получить доступ только при отсутствии работающих писателей.
Запросы на доступ должны удовлетворяться “справедливо” - в порядке их поступления (можно исходить из “справедливости“ удовлетворения запросов на двоичные семафоры).
Ответ:
semaphore sem_r = 1, sem_ra = 1, sem_w = 1;
int readers_count = 0;
r_enter() { // Читатель хочет начать читать
sem_r.P();
sem_ra.P();
++readers_count;
if (readers_count == 1)
sem_w.P(); // Первый читатель блокирует возможность писать
sem_ra.V();
sem_r.V();
}
r_leave() { // Читатель выходит из области чтения
sem_ra.P();
--readers_count;
if (readers_count == 0)
sem_w.V(); // Последний читатель освобождает семафор
sem_ra.V();
}
w_enter() { // Писатель хочет писать
sem_r.P(); // Чтобы новые читатели не начинали читать и чтобы
// избежать блокировки при одновременном входе читателя и писателя.
sem_w.P();
}
w_leave() { // Писатель выходит из области записи
sem_w.V();
sem_r.V();
}
[править] Тема 3
[править] Задача 1 (MPI_BARRIER)
В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо выполнить операцию барьер (MPI_BARRIER) для всех процессов. Сколько времени потребуется для этого, если все процессы выдали ее одновременно. Время старта равно Ts, время передачи байта равно Tb (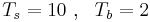 ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ: MPI_Barrier останавливает выполнение вызвавшей ее задачи до тех пор, пока не будет вызвана изо всех остальных задач, подсоединенных к указываемому коммуникатору. Гарантирует, что к выполнению следующей за MPI_Barrier инструкции каждая задача приступит одновременно с остальными.
[править] Задача 2 (MPI_BCAST)
В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо выполнить операцию передачи сообщения длиной N байт всем процессам от одного (MPI_BCAST) - процесса с координатами (0,0). Сколько времени потребуется для этого, если все процессы выдали ее одновременно. Время старта равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
Без конвейера: Операция MPI_BCAST осуществляет посылку сообщений всем соседям данного транспьютера. Следовательно, каждая посылка сообщения в транспьютерной матрице операцией (MPI_BCAST) заполняет очередную диагональ матрицы: 0 - (0, 0); 1 - (1, 0), (0, 1); 2 - (2, 0), (1, 1), (0, 2) и т.д (где (i, j) - координата процесса). Следовательно, для осуществения операции MPI_BCAST в матрице 4x4 нужно 6 * (Ts + N*Tb) единиц времени.
С конвейером (но, наверное, неправильно): А если разбить сообщение на байты и передавать конвейерно: тогда потребуется 6*Ts на инициализацию узлов, 6*Tb на инициализацию конвейера (предположим, что маршрут один), и (N-1)*Tb для передачи всего сообщения.
Небольшой комментарий:
Для конвейера неправильно.
Исходим из определения времени старта: Время старта-время инициализации канала для передачи любого количества данных (хоть одного байта)
Разобьем сообщение на К кусков.
Время передачи первого куска до последней точки (3,3) (загрузка конвейера) равно 6*(Ts+Tb*N/K) (см. пункт без конвейера)
Время прохода остальных кусков (конвейер загружен) (K-1)*(Ts+Tb*N/K)
ИТОГО: 6*(Ts+Tb*N/K)+(K-1)*(Ts+Tb*N/K)
Для особых эстетов минимум достигается при K = [sqrt( 5 * Tb * N / Ts)]
[править] Задача 3 (MPI_GATHER)
В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо выполнить операцию сбора данных от всех процессов (длиной один байт) для одного (MPI_GATHER) - процесса с координатами (0,0). Сколько времени потребуется для этого, если все процессы выдали ее одновременно. Время старта равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
Матрица 4*4 и собирающий узел - (0,0), значит входящих каналов 2. Передающих узлов 15, каналов 2, значит минимальное количество тактов передач - 8. И её просто достичь, передавая сообщения по двум конвейерным маршрутам. Итого: Если считать, что узлы не могут накапливать информацию, то потребуется 8 тактов инициализаций и 8 тактов синхронных передач. 8*Ts+8*Tb
[править] Задача 4 (MPI_SCATTER)
В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо выполнить операцию рассылки данных (длиной один байт) всем процессам от одного (MPI_SCATTER) - процесса с координатами (0,0). Сколько времени потребуется для этого, если все процессы выдали ее одновременно. Время старта равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
Похоже, что эта задача отличается от предыдущей только направлением потока данных. Так что ответ такой же.
[править] Задача 5 (суммирование)
В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо выполнить операцию суммирования 16 чисел (каждый процесс имеет свое число). Сколько времени потребуется для получения всеми суммы, если все процессы выдали эту операцию редукции одновременно? А сколько времени потребуется для суммирования 64 чисел в матрице 8*8? Время старта равно единице, время передачи байта равно нулю (Ts=1,Tb=0). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
Пусть никакой буферизации не предусмотрено. Для получения суммы на одном из четырёх центральных процессов ((1,1),(2,1),(1,2),(2,2)) необходимо 4 операции (2 операции для получения суммы своего угла из 4 процессов для каждого центрального процесса, ещё две, чтобы получить общую сумму на всех - на каждом такте складываем сумму на транспьтере с соседями (к примеру, (1,1) с (2,1) и (1, 2). После этого на каждом из 4х транспьютеров получается удвоенная сумма, из которой получается просто сумма) Неправильно, при таких операциях получатся числа вида 3a+2b+2c+2d, 2a+3b+2c+2d и т. п.. На самом деле нужно на первом такте (3) переслать числа по вертикали (от (2,1) к (3,1) и обратно, от (2,2) к (3,2) и обратно, при этом каждый прибавляет полученное значение к своему, так получатся a+c, c+a и b+d, d+b. На втором такте (4) – аналогично по горизонтали, получится полная сумма во всех четырех вершинах). Затем нужно ещё 2 операции, чтобы разослать информацию во все углы. Итого: 6*(Ts+Tb).
Если процессов 64, то разобьём квадрат на 4 подквадрата. Как было показано ранее, за 4 операции пожно получить сумму своего квадрата в (2,2), (5,2), (2,5) и (5,5). Ещё две операции нужно на пересылку в центральные процессы. Там за 2 операции получаем сумму на всех из них (как и в первом случае), и ещё 6 на рассылку. Итого: 14*(Ts+Tb).
[править] Задача 6 (максимум)
В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо выполнить операцию нахождения максимума среди 16 чисел (каждый процесс имеет свое число). Сколько времени потребуется для получения всеми максимального числа, если все процессы выдали эту операцию редукции одновременно. А сколько времени потребуется для нахождения максимума среди 64 чисел в матрице 8*8? Время старта равно единице, время передачи байта равно нулю (Ts=1,Tb=0). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
Концептуально задача не отличается от предыдущей. Ответ тот же.
[править] Задача 7 (передача сообщения)
В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо переслать очень длинное сообщение (длиной L байт) из узла с координатами (0,0) в узел с координатами (3,3). Сколько времени потребуется для этого? А сколько времени потребуется для пересылки из узла с координатами (1,1) в узел с координатами (2,2)? Время старта равно времени передачи байта (Ts=Tb). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
В задаче 3.2 был получен результат 6*(Ts+Tb*L/K)+(K-1)*(Ts+Tb*L/K). При передаче из одного в угла другой можно получить то же время, деля это длинное сообщение на K кусков. Кроме того, его можно распилить пополам и пустить двумя путями (больше не получится -- около углов узкое место), тогда время будет такое: 6*(Ts+Tb*L/(2K))+(K-1)*(Ts+Tb*L/(2K)).
С передачей из (1,1) в узел с координатами (2,2) немного сложнее. Строго говоря, там возможны 4 пути: два длины 2 и два длины 6. Пусть есть N - часть сообщения L, которую мы пустим по коротким каналам. Тогда 0.5L < N < L из соображений здравого смысла, и будем N дробить на K1 частей, а (L-N) на K2 частей. Тогда получаем формулу:
- max{ 2*(Ts+Tb*N/(2K1))+(K1-1)*(Ts+Tb*N/(2K1)), 6*(Ts+Tb*(L-N)/(2K2))+(K2-1)*(Ts+Tb*(L-N)/(2K2)) }.
И эту жесть надо минимизировать по N, K1, K2.
Ответ (вариант 2):
На консультации сказали, что если в задании есть слова очень длинное сообщение, то можно пренебречь временем старта, временем разгона конвейера и длиной маршрута. Таким образом, у нас остается только Tb. Тогда из (0,0) в (3,3) можно переслать сообщение за время L*Tb/2 (т. к. возможно два маршрута), из (1,1) в (2,2) -- за время L*Tb/4 (т. к. в этом случае 4 маршрута).
[править] Задача 8 (буферизуемая передача сообщения)
В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо переслать сообщение длиной L байт из узла с координатами (0,0) в узел с координатами (3,3). Сколько времени потребуется для этого, если передача сообщений выполняется в буферизуемом режиме MPI? А сколько времени потребуется при использовании синхронного режима и режима готовности? Время старта равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ: Если все транспьютеры готовы к приёму, то ничем не отличается от предыдущих задач (если хочется учитывать квитанции, надо добавлять, например, посылку-приём байта перед передачей содержательной информации).
[править] Задача 9 (блокирующая/неблокирующая передача сообщения)
В транспьютерной матрице размером 4*4, в каждом узле которой находится один процесс, необходимо переслать сообщение длиной L байт из узла с координатами (0,0) в узел с координатами (3,3). Сколько времени потребуется для этого при использовании а) неблокирующих и б) блокирующих операций MPI? Время старта равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ: Блокирующие и неблокирующие операции по времени ничем не должны отличаться. Поэтому решется аналогично задачам, описанным выше.
[править] Тема 4
[править] Задача 1 (Круговой маркерный алгоритм)
1. Все 16 процессов, находящихся в узлах транспьютерной матрицы размером 4*4, одновременно выдали запрос на вход в критическую секцию. Сколько времени потребуется для прохождения всеми критических секций, если используется круговой маркерный алгоритм. Время старта равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ: Все процессы составляют логическое кольцо, когда каждый знает, кто следует за ним. По кольцу циркулирует маркер, дающий право на вход в критическую секцию. Получив маркер (посредством сообщения точка-точка) процесс либо входит в критическую секцию (если он ждал разрешения) либо переправляет маркер дальше. После выхода из критической секции маркер переправляется дальше, повторный вход в секцию при том же маркере не разрешается. 15*(Ts + 1*Tb)
[править] Задача 2 (Древовидный маркерный алгоритм)
2. Все 16 процессов, находящихся на разных ЭВМ сети с шинной организацией (без аппаратных возможностей широковещания), одновременно выдали запрос на вход в критическую секцию. Сколько времени потребуется для прохождения всеми критических секций, если используется древовидный маркерный алгоритм. Время старта (время разгона после получения доступа к шине) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
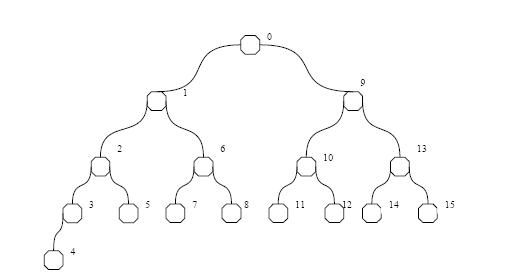
Составляем сбалансированное дерево, например, такое. Где бы ни находился маркер, нужно 15 посылок запросов для инициализации (по каждому ребру либо в обну, либо в другую сторону). Далее, надо, начиная с вершины, где есть маркер, обойти в глубину дерево. Кажется, что оптимально это можно сделать за 26 операций. В самом деле, начнём обход из корня (0), и будем обходить сначала правые поддеревья, потом левые. Тогда по каждому ребру придётся пройти 2 раза (вперёд и назад), кроме последних четырёх(рёбра 0-1, 1-2, 2-3, 3-4), так как из вершины 4 маркер возвращаться не будет (очередь пуста). Итого: (15+26)(Ts+1*Tb).
Замечание: в приведенном выше решении, на мой взгляд, имеется ошибка - не учтены повторные посылки запроса после того, как маркер покидает вершину, в направлении ушедшего маркера (они выполняются, если очередь запросов в узле не пуста). Их количество считается вручную (мысленно проводим обход дерева и при каждом переходе в следующую вершину смотрим, остались ли еще запросы на только что покинутой). На приведенном выше рисунке, таким образом, строя обход в глубину справа налево, нужно к ответу добавить 11*(Ts+1*Tb). Данное решение принято аспирантом на экзамене, кроме того, им было сделано замечание, что запрос может посылаться вместе с маркером в одном сообщении, тогда удастся избежать лишних накладных расходов на инициацию передачи и к ответу добавится просто 11*Tb.
Замечание2: А если начать обход не с 0 вершины, а с 15? тогда нам потребуется только 23 операции (т.к не придется дважды проходить 15-13, 13-9, 9-0)
[править] Задача 3 (Децентрализованный алгоритм с временными метками)
3. Все 16 процессов, находящихся на разных ЭВМ сети с шинной организацией (без аппаратных возможностей широковещания), одновременно выдали запрос на вход в критическую секцию. Сколько времени потребуется для прохождения всеми критических секций, если используется децентрализованный алгоритм с временными метками. Время старта (время «разгона» после получения доступа к шине для передачи сообщения) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса на передачу (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память, считаются бесконечно быстрыми.
Ответ:
Каждый процесс шлет запрос на вход в критическую секцию всем остальным 15 процессам. Итого: 15*16*(Ts+Tb*L)
После выполнения критической секции процесс смотрит свои запросы на вход в своем списке и шлет им Ok.
В результате на посылку Ok уходит 15*16*(Ts+Tb*Lok)
Итого: 15*16*(2Ts+Tb*(L+Lok))
[править] Задача 4 (Широковещательный маркерный алгоритм)
Все 16 процессов, находящихся на разных ЭВМ сети с шинной организацией (без аппаратных возможностей широковещания), одновременно выдали запрос на вход в критическую секцию. Сколько времени потребуется для прохождения всеми критических секций, если используется широковещательный маркерный алгоритм (маркером владеет нулевой процесс). Время старта равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Процессорные операции, включая чтение из памяти и запись в память, считаются бесконечно быстрыми.
Ответ:
Маркер находится у процесса 0. Он спокойно входит в КС, а все остальные шлют broadcast запросы о желании войти в КС. Им нужно для этого 15*16 тактов, так как нет аппаратной поддержки широковещания. После этого у маркера сформировалась очередь из 15 желающих войти в КС, и он по очереди удовлетворяет их желания (на каждое нужна одна пересылка маркера). Всего получается 15*16+15 тактов. Можно чередовать операции рассылки и передачи маркера, но их всё равно будет столько же. Ответ: 15*16*(Ts+Tb*Lreq) + 15*(Ts+Tb*Lmark).
Заметьте, что здесь Lmark довольно большая. В сообщение должны помещаться очередь длины 1..15 и массив из 16 номеров последних запросов.
[править] Задача 5 (Централизованный алгоритм)
5. 15 процессов, находящихся в узлах транспьютерной матрицы размером 4*4, одновременно выдали запрос на вход в критическую секцию. Сколько времени потребуется для прохождения всеми критических секций, если используется централизованный алгоритм (координатор расположен в узле 0,0)? Время старта равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
Как известно, для обработки КС централизованным алгоритмом нужно 3 сообщения (запрос, разрешение, подтверждение окончания). Всего от всех процессов до (0,0) нужно совершить 48 переходов (2*1 + 3*2 + 4*3 + 3*4 + 2*5 + 6). Значит, всего потратим времени 3*48*(Ts+Tb).
Комментарий: Сбор запросов происходит параллельно, а т.к. канала 2 - понадобится 15 / 2 = 8 тактов, итого получим (8+2*48)(Ts+Tb).
[править] Задача 6 (Алгоритм задиры)
6. Сколько времени потребует выбор координатора среди 16 процессов, находящихся на разных ЭВМ сети с шинной организацией (без аппаратных возможностей широковещания), если используется алгоритм «задиры»? «Задира» расположен в узле с координатами (0,0) и имеет уникальный номер 0. Время старта (время «разгона» после получения доступа к шине для передачи сообщения) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса на передачу (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память, считаются бесконечно быстрыми.
Ответ: Так как задирой является процесс с наименьшим номером, то он пошлет сообщение ВЫБОРЫ всем остальным процессам и получит от всех ответ ОК. После этого все остальные процессы будут инициировать выборы, рассылая сообщения процессам с бОльшими номерами и получая ответы. Процесс же с наибольшмим номером (15) разошлет всем сообщения КООРДИНАТОР, тем самым закончив выборы. Итого: (1 + 2 + ... + 15)(Ts + Tb * Lvybory) + (1 + 2 + ... + 15)(Ts + Tb * Lok) + 15(Ts + Tb * Lcoordinator) = 120(2Ts + Tb(Lvybory + Lok)) + 15(Ts + Tb * Lcoordinator)
[править] Задача 7 (Круговой алгоритм)
7. Сколько времени потребует выбор координатора среди 16 процессов, находящихся в узлах транспьютерной матрицы размером 4*4, если используется круговой алгоритм? Время старта равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
Инициатор посылает сообщение ВЫБОРЫ со своим номером следующему по кругу. Следующий живой процесс добавляет свой номер и посылает дальше. Так, пока не будет пройден круг (процесс увидел в сообщении свой номер). Тогда он выбирает максимальный номер и посылает сообщение КООРДИНАТОР с этим номером, оповещая о новом координаторе. Всего получается два круга сообщений. Итого: 16*(Ts + Tb*Lvibory) + 16*(Ts + Tb*Lcoordinator).
[править] Тема 5
1. Какие принципиальные решения приходится принимать при обеспечении файлового сервиса?
Ответ:
- Есть ли разница между клиентами и серверами? Имеются системы, где все машины имеют одно и то же ПО и любая машина может предоставлять файловый сервис. Есть системы, в которых серверы являются обычными пользовательскими процессами и могут быть сконфигурированы для работы на одной машине с клиентами или на разных. Есть системы, в которых клиенты и серверы являются фундаментально разными машинами с точки зрения аппаратуры или ПО.
- Должны ли быть файловый сервер и сервер директорий отдельными серверами или быть объединенными в один сервер. Разделение позволяет иметь разные серверы директорий (UNIX, MS-DOS) и один файловый сервер. Объединение позволяет сократить коммуникационные издержки.
- Должны ли серверы хранить информацию о клиентах. См. вопрос про сервер с состоянием.
2. Интерфейс сервера директорий.
Ответ:
Обеспечивает операции создания и удаления директорий, именования и переименования файлов, перемещение файлов из одной директории в другую.
Определяет алфавит и синтаксис имен. Для спецификации типа информации в файле используется часть имени (расширение) либо явный атрибут.
Все распределенные системы позволяют директориям содержать поддиректории - такая файловая система называется иерархической. Некоторые системы позволяют создавать указатели или ссылки на произвольные директории, которые можно помещать в директорию. При этом можно строить не только деревья, но и произвольные графы (разница между ними очень важна для распределенных систем, поскольку в случае графа удаление связи может привести к появлению недостижимых поддеревьев. Обнаруживать такие поддеревья в распределенных системах очень трудно).
Ключевое решение при конструировании распределенной файловой системы - должны или не должны машины (или процессы) одинаково видеть иерархию директорий. Тесно связано с этим решением наличие единой корневой директории (можно иметь такую директорию с поддиректориями для каждого сервера).
Прозрачность именования. Две формы прозрачности именования различают - прозрачность расположения (/server/d1/f1) и прозрачность миграции (когда изменение расположения файла не требует изменения имени).
Имеются три подхода к именованию:
* машина + путь;
* монтирование удаленных файловых систем в локальную иерархию файлов;
* единственное пространство имен, которое выглядит одинаково на всех машинах.
Последний подход необходим для достижения того, чтобы распределенная система выглядела как единый компьютер, однако он сложен и требует тщательного проектирования.
3. Семантика разделения файлов.
Ответ:
- UNIX-семантика --- естественная семантика однопроцессорной ЭВМ - если за операцией записи следует чтение, то результат определяется последней из предшествующих операций записи. В распределенной системе такой семантики достичь легко только в том случае, когда имеется один файл-сервер, а клиенты не имеют кэшей. При наличии кэшей семантика нарушается. Надо либо сразу все изменения в кэшах отражать в файлах, либо менять семантику разделения файлов.
- Неизменяемые файлы --- очень радикальный подход к изменению семантики разделения файлов. Только две операции - создать и читать. Можно заменить новым файлом старый - т.е. можно менять директории. Если один процесс читает файл, а другой его подменяет, то можно позволить первому процессу доработать со старым файлом в то время, как другие процессы могут уже работать с новым.
- Семантика сессий --- изменения открытого файла видны только тому процессу (или машине), который производит эти изменения, а лишь после закрытия файла становятся видны другим процессам (или машинам). Что происходит, если два процесса одновременно работали с одним файлом - либо результат будет определяться процессом, последним закрывшим файл, либо можно только утверждать, что один из двух вариантов файла станет текущим.
- Транзакции --- процесс выдает операцию “НАЧАЛО ТРАНЗАКЦИИ”, сообщая тем самым, что последующие операции должны выполняться без вмешательства других процессов. Затем выдает последовательность чтений и записей, заканчивающуюся операцией “КОНЕЦ ТРАНЗАКЦИИ”. Если несколько транзакций стартуют в одно и то же время, то система гарантирует, что результат будет таким, каким бы он был в случае последовательного выполнения транзакций (в неопределенном порядке). Пример - банковские операции.
4. Серверы с состоянием и без состояния. Достоинства и недостатки.
Ответ:
Серверы с состоянием. Достоинства.
- Короче сообщения (двоичные имена используют таблицу открытых файлов).
- выше эффективность (информация об открытых файлах может храниться в оперативной памяти).
- блоки информации могут читаться с упреждением.
- убедиться в достоверности запроса легче, если есть состояние (например, хранить номер последнего запроса).
- возможна операция захвата файла.
Серверы без состояния. Достоинства.
- устойчивость к ошибкам.
- не требуется операций ОТКРЫТЬ/ЗАКРЫТЬ.
- не требуется память для таблиц.
- нет ограничений на число открытых файлов.
- нет проблем при крахе клиента.
5. Алгоритмы обеспечения консистентности кэшей в распределенных файловых системах.
Ответ:
- Алгоритм со сквозной записью. Необходимость проверки, не устарела ли информация в кэше. Запись вызывает коммуникационные расходы (MS-DOS).
- Алгоритм с отложенной записью. Через регулярные промежутки времени все модифицированные блоки пишутся в файл. Эффективность выше, но семантика непонятная пользователю (UNIX).
- Алгоритм записи в файл при закрытии файла. Реализует семантику сессий. Не намного хуже случая, когда два процесса на одной ЭВМ открывают файл, читают его, модифицируют в своей памяти и пишут назад в файл.
- Алгоритм централизованного управления. Можно выдержать семантику UNIX, но не эффективно, ненадежно, и плохо масштабируется.
6. Способы организации размножения файлов и коррекции копий.
Ответ:
Система может предоставлять такой сервис, как поддержание для указанных файлов нескольких копий на различных серверах. Главные цели:
- Повысить надежность.
- Повысить доступность (крах одного сервера не вызывает недоступность размноженных файлов.
- Распределить нагрузку на несколько серверов.
- Явное размножение (непрозрачно). В ответ на открытие файла пользователю выдаются несколько двоичных имен, которые он должен использовать для явного дублирования операций с файлами.
- “Ленивое” размножение. Одна копия создается на одном сервере, а затем он сам автоматически создает (в свободное время) дополнительные копии и обеспечивает их поддержание.
- Симметричное размножение. Все операции одновременно вызываются в нескольких серверах и одновременно выполняются.
Протоколы коррекции. Просто посылка сообщений с операцией коррекции каждой копии является не очень хорошим решением, поскольку в случае аварий некоторые копии могут остаться не скорректированными. Имеются два алгоритма, которые решают эту проблему.
- Метод размножения главной копии. Один сервер объявляется главным, а остальные - подчиненными. Все изменения файла посылаются главному серверу. Он сначала корректирует свою локальную копию, а затем рассылает подчиненным серверам указания о коррекции. Чтение файла может выполнять любой сервер. Для защиты от краха главного сервера до завершения всех коррекций, до выполнения коррекции главной копии главный сервер запоминает в стабильной памяти задание на коррекцию. Слабость - выход из строя главного сервера не позволяет выполнять коррекции.
- Метод голосования. Идея - запрашивать чтение и запись файла у многих серверов (запись - у всех!). Запрос может получить одобрение у половины серверов плюс один. При этом должно быть согласие относительно номера текущей версии файла. Этот номер увеличивается на единицу с каждой коррекцией файла. Можно использовать различные значения для кворума чтения (Nr) и кворума записи (Nw). При этом должно выполняться соотношение Nr+Nw>N. Поскольку чтение является более частой операцией, то естественно взять Nr=1. Однако в этом случае для кворума записи потребуются все серверы.
[править] Тема 6 (задачи на консистентность)
Общий хинт - в Таненбауме "Распределенные системы" расписано, как реализуется та или иная консистентность в главе 6. Нужно аккуратно посмотреть какие и куда будут пересылки сообщений при такой консистентности.
При ответах на вопросы по теме 6 следовать следующему плану.
- Определение модели консистентности.
- Алгоритм реализации в DSM с полным размножением (много писателей и много читателей, каждый из которых имеет свою копию всех переменных). Алгоритм должен быть корректным для любой коммуникационной сети и обеспечивать высокую эффективность для конкретной сети, указанной в задаче. Описание алгоритма должно содержать ответы на следующие вопросы:
- что делается при записи;
- что делается при чтении;
- когда, кому и как рассылаются значения модифицируемых переменных;
- блокируется ли процесс на время выполнения записи или рассылки значений переменных;
- если речь идет о моделях консистентности, связанных с синхронизацией, то объяснить алгоритм синхронизации (например, алгоритм входа в КС и выхода из нее).
- Оценить время работы описанного в пункте 2 алгоритма применительно к конкретной задаче.
[править] Последовательная
Последовательная консистентность памяти и алгоритм ее реализации в DSM с полным размножением. Сколько времени потребует модификация 10 различных переменных 10-ю процессами (каждый процесс модифицирует одну переменную), находящимися на разных ЭВМ сети с шинной организацией (без аппаратных возможностей широковещания) и одновременно выдавшими запрос на модификацию. Время старта (время разгона после получения доступа к шине) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
[править] Причинная
Причинная консистентность памяти и алгоритм ее реализации в DSM с полным размножением. Сколько времени потребует модификация 10 различных переменных, если все 10 процессов (каждый процесс модифицирует одну переменную), находящихся на разных ЭВМ сети с шинной организацией (без аппаратных возможностей широковещания), одновременно выдали запрос на модификацию своей переменной. Время старта (время разгона после получения доступа к шине) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми. Никаких сведений от компилятора о причинной зависимости операций модификации не имеется.
Ответ:
[править] PRAM
PRAM консистентность памяти и алгоритм ее реализации в DSM с полным размножением. Сколько времени потребует 3-кратная модификация 10 различных переменных, если все 10 процессов (каждый процесс 3 раза модифицирует одну переменную), находящихся на разных ЭВМ сети с шинной организацией (без аппаратных возможностей широковещания), одновременно выдали запрос на модификацию. Время старта (время разгона после получения доступа к шине) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ: Семантике PRAM консистентности больше соответствует алгоритм с координатором — при записи в переменную соответствующий процесс посылает изменение координатору, а сам продолжает работу. Тем не менее, поскольку записи одного процесса должны видеться всеми остальными процессами в одном порядке, придётся учитывать и время рассылки обновлений от координатора к остальным процессам. Итак, если процесс, изменяющий переменную, не совпадает с координатором, то при каждом изменении переменной потребуется (Ts + Tb * l1) на отправку изменённого значения координатору и ещё (N − 2) * (Ts + Tb * l2) на рассылку нового значения остальным процессам от координатора (где N — число процессов; процессу, изначально изменившему переменную, и координатору не надо рассылать новое значение по шине). Если же процесс-модификатор переменной совпадает с координатором, то (Ts + Tb * l1) уже не нужно, зато нужно (N − 1) * (Ts + Tb * l2) на рассылку. Ещё необходимо учесть, что каждый процесс меняет переменную трижды. Итого получается 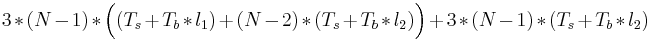 , т.е.
, т.е. 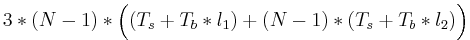 .
.
Алгоритм без координатора также возможен — в этом случае процессу-модификатору самому необходимо рассылать остальным N-1 процессам новые значения переменной после её модификации. Всего в этом случае потребуется 3 * N * (N − 1) * (Ts + Tb * l2).
[править] Процессорная
Процессорная консистентность памяти и алгоритм ее реализации в DSM с полным размножением. Сколько времени потребует модификация 10 различных переменных, если все 10 процессов (каждый процесс модифицирует одну переменную), находящихся на разных ЭВМ сети с шинной организацией (без аппаратных возможностей широковещания), одновременно выдали запрос на модификацию своей переменной. Время старта (время разгона после получения доступа к шине) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ: Поскольку процессорная консистентность — это PRAM + когерентность памяти, то нам необходимо, чтобы процессы, прежде чем редактировать переменные, сначала посылали запросы к коррдинатору, а уже после согласия коодинатора изменяли их (важно!). Затем, в реализации процессорной консистентности нам не обойтись без координаторов, в результате получаем два случая: когда у каждой переменной по координатору и когда 1 координатор отвечает за все переменные.
1 случай: много координаторов. Предположим, что для каждой переменной тот процесс, который её изменяет, является её же координатором. Тогда, процессам не нобходимо посылать никакие запросы (всё это происходит внутри процесса), необходимо только уведомлять другие процессы о совершенных изменениях. В итоге получаем: каждый из N процессов рассылает остальным (N-1) процессам уведомления об изменениях. Ответ: N * (N − 1) * (Ts + Tb * L)
2 случай: 1 координатор. Итак, если процесс, изменяющий переменную, не совпадает с координатором, то посл-ть такова: при запросе записи в переменную соответствующий процесс посылает сообщение координатору, (Ts + Tb * Lzapr), затем получает подтверждение от него (Ts + Tb * Lok), процесс изменяет переменную и шлёт изменение координатору (Ts + Tb * Lnew2coord), а тот уже рассылает остальным изменения: (N − 2) * (Ts + Tb * Lnew2all). Если же процесс-модификатор переменной совпадает с координатором, то требуется только уведомление остальных процессов об изменении переменной: (N − 1) * (Ts + Tb * Lnew2all) на рассылку. Суммируем, и, учитывая кол-во процессов, получаем: 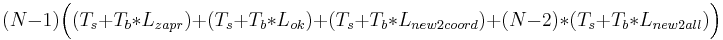 и (N − 1) * (Ts + Tb * Lnew2all).
и (N − 1) * (Ts + Tb * Lnew2all).
Ответ: 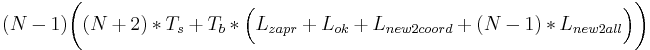 .
.
[править] Слабая
Слабая консистентность памяти и алгоритм ее реализации в DSM с полным размножением. Сколько времени потребует модификация одним процессом 10 обычных переменных, а затем 3-х различных синхронизационных переменных, если DSM реализована на 10 ЭВМ сети с шинной организацией (с аппаратными возможностями широковещания). Время старта (время разгона после получения доступа к шине для передачи) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
[править] По выходу
Консистентность памяти по выходу и алгоритм ее реализации в DSM с полным размножением. Сколько времени потребует трехкратное выполнение критической секции и модификация в ней 10 переменных каждым процессом , если DSM реализована на 10 ЭВМ сети с шинной организацией (с аппаратными возможностями широковещания). Время старта (время разгона после получения доступа к шине для передачи) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ: У нас 10 ЭВМ. Широковещательный доступ. Консистентность по входу - мы можем как угодно разбить переменные на блоки, которые будут защищаться синх.переменными. Поэтому, пусть критическая секция будет под одной переменной.
При захвате переменной ЭВМ посылает всем широковещательный запрос на захват. Все должны ответить ОК. Тогда переменная наша и можно все менять.
Если переменная у нас, то собираем очередь запросов. ЗАкончили работу, теперь надо сделать широковещательную рассылку новых данных. И только после этого послылаем сообщение первому в очереди с ОК и (как мне кажется) передаем ему очередь запросов.
(Ts + Tb * Lzapr) + // запрос
9 * (Ts + Tb * Lok) + //все должны ответить
(Ts + Tb * Lv)// время на синхронизацию на выходе.
Итого: 10 * 3 * (10 * Ts + Tb * (Lzapr + 9 * Lok + Lv))
[править] По входу
Консистентность памяти по входу и алгоритм ее реализации в DSM с полным размножением. Сколько времени потребует трехкратное выполнение критической секции и модификация в ней 11 переменных каждым процессом, если DSM реализована на 10 ЭВМ сети с шинной организацией(с аппаратными возможностями широковещания). Время старта (время разгона после получения доступа к шине для передачи) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Примечание: решение не верное, лектор сказал надо использовать какой-нибудь алгоритм с маркером.
Ответ: Консистентность памяти по входу (она же поэлементная в Таненбауме), закрепляет каждую разделяемую переменную за своей синхронизационной переменной. Поэтому для изменения каждой переменной необходимо производить свой захват и освобождение синхронизационной переменной. Так как Крюков сказал, что нужны децентрализованные алгоритмы, пользуемся таким.
Для захвата переменной процесс посылает широковещательный запрос. Все остальные отвечают ему. Если процесс не владеет синхронизационной переменной, то сразу отвечает ОК, если владеет, то после освобождения синх.переменной он должен послать ответ ОК и новое значение разделяемой переменной. Итого, один захват синх.переменной требует (Ts + Tb * Lzapr) + 8 * (Ts + Tb * Lok) + (Ts + Tb * (Lok + Lv)) = 10 * Ts + Tb * (Lzapr + 9 * Lok + Lv).
Все захваты для всех 11 переменных для трех критических секций для 10 ЭВМ ничем не отличаются друг от друга. Поэтому общий ответ: 10 * 3 * 11 * (10 * Ts + Tb * (Lzapr + 9 * Lok + Lv)).
[править] Алгоритм Деккера
Какие модели консистентности памяти удовлетворяют алгоритму Деккера (алгоритм без каких-либо изменений будет работать правильно), а какие нет? Объясните ответ.
Ответ: не слабее последовательной консистентности. При последовательной консистентности невозможно, чтобы оба процесса прочли false, читая флаги другого процесса. Таким образом требование того, что в критической секции не могут одновременно находиться находиться оба процесса, выполнение. Тупика тоже для модели последовательной консистентности не будет
[править] Алгоритм Петерсона
Какие модели консистентности памяти удовлетворяют алгоритму Петерсона (алгоритм без каких-либо изменений будет работать правильно), а какие нет? Объясните ответ.
Ответ:
[править] Тема 7
1. Проблемы бесконечного восстановления и потери сообщений. Какие методы их решения существуют? Дайте оценку накладных расходов для сети из 10 ЭВМ с шинной организацией (без аппаратных возможностей широковещания). Время старта (время разгона после получения доступа к шине для передачи) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
2. Консистентное и строго консистентное множество контрольных точек и алгоритмы их фиксации. Дайте оценку накладных расходов на синхронную фиксацию строго консистентного множества контрольных точек для сети из 12 ЭВМ с шинной организацией (без аппаратных возможностей широковещания), если расходы на синхронную фиксацию консистентного множетва точек составляют T1. Время старта (время разгона после получения доступа к шине для передачи) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Операции с файлами и процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ: Сначала прогоняем синхронную фиксацию консистентного множества КТ. Это потребует T1. Эти контрольные точки будем считать промежуточными.
Исходя из определения, для того, чтобы консистентное множество точек стало строго консистентным, надо убедиться, что между процессами нет никаких сообщений. Для этого мы можем просто пропустить по всем каналам свои собственные сообщения. Если они все пройдут, значит, каналы пусты и множество строго консистентно. Однако, стоит обратить внимание, что координатор уже посылал всем служебные сообщения, так что его каналы проверять не нужно. У нас остается 11 ЭВМ, которые хотят проверить по 10 каналов каждая. ЭВМ запоминают, по каким каналам им приходят эти служебные сообщения. Если придут по всем 10, посылают сообщение координатору с указанием того, что они готовы к созданию точки. Если координатору придут все сообщения, он рассылает уведомление о фиксации множества.
Примечание: n(n-1) - плохая оценка, надо не проверять все каналы, а просто считать отосланные сообщения
Итак, по полочкам:
T = T1 // консистентное множество
+ 11*10*(Ts + Tb * L) // посылка служебных сообщений
+ 11*(Ts + Tb * L_ok) // уведомление координатора о готовности
+ 11*(Ts + Tb * L_coord) // фиксация множества
3. Протоколы голосования. Алгоритмы и применение. Дайте оценку времени выполнения одним процессом 2-х операций записи и 10 операций чтения одного байта информации с файлом, размноженным на остальных 10 ЭВМ сети с шинной организацией (без аппаратных возможностей широковещания). Определите оптимальные значения кворума чтения и кворума записи. Время старта (время разгона после получения доступа к шине для передачи) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Операции с файлами и процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
4. Алгоритм надежных и неделимых широковещательных рассылок сообщений. Дайте оценку времени выполнения одной операции рассылки для сети из 10 ЭВМ с шинной организацией (без аппаратных возможностей широковещания). Время старта (время разгона после получения доступа к шине для передачи) равно 100, время передачи байта равно 1 (Ts=100,Tb=1). Доступ к шине ЭВМ получают последовательно в порядке выдачи запроса (при одновременных запросах - в порядке номеров ЭВМ). Процессорные операции, включая чтение из памяти и запись в память считаются бесконечно быстрыми.
Ответ:
[править] Прочие вкусности от лектора
1. Какую модель консистентности можно реализовать в мультипроцессорах (с общей памятью)?
Ответ:
Последовательную. Строгую не можем, так как у процессоров имеется кэш.
2. MPI. В синхронизационном режиме отправка сообщения не начинается, пока у процесса, который должен принять сообщение, не появится RECEIVE. А как мы это узнаем?
Ответ:
Процесс, в котором появился SEND, должен отправить запрос, есть ли на другом конце RECEIVE. Это должен сделать именно он, так как:
- он знает получателя (второй процесс может не знать отправителя),
- он знает, что отправка будет производиться в синхронизационном режиме (получатель не может и не должен знать режим).
3. Зачем в задаче 2.4 необходимо наличие возможности прерывания, ведь и без него, казалось бы, всё можно реализовать?
Ответ:
[править] Задачи из лекций Вали Глазковой
[править] Задача 1
Реализовать модель причинной консистентности без сервера и упорядоченного широковещания.
Если верить дядюшке Таненбауму нужен граф зависимостей операций и алгоритм его обхода. см. "Распределенные системы", Таненбаум, глава 6, Причинная консистентность.
[править] Задача 2
Пример "смерти процессов" возможен для PRAM консистентонсти и невозможен для последовательной. Возможен ли он для причинной консистентности?
[править] Задача 3
Написать алгоритмы Деккера и Петерсона.
Алгоритм Деккера (enwiki)
Суть алгоритма -- не дать двум параллельным процессам одновременно войти в критическую секцию.
flag[0] := false
flag[1] := false
turn := 0 // or 1
p0: p1:
flag[0] := true flag[1] := true
while flag[1]=true { while flag[0]=true {
if turn ≠ 0 { if turn ≠ 1 {
flag[0] := false flag[1] := false
while turn ≠ 0 { while turn ≠ 1 {
} }
flag[0] := true flag[1] := true
} }
} }
// critical section // critical section
... ...
// remainder section // remainder section
turn := 1 turn := 0
flag[0] := false flag[1] := false
Алгоритм Петерсона (enwiki)
flag[0] = 0
flag[1] = 0
turn = 0
P0: flag[0] = 1 P1: flag[1] = 1
turn = 1 turn = 0
while( flag[1] && turn == 1 ); while( flag[0] && turn == 0 );
// do nothing // do nothing
// critical section // critical section
... ...
// end of critical section // end of critical section
flag[0] = 0 flag[1] = 0
[править] Задача 4
Читатель не должен читать сырые данные. Читать могут сразу много. Писать – только один.
Int rd = 0; // количество читателей
Semaphore access = 1;
Semaphore reader = 1; // семафор для читателей
Semaphore writer = 1; // семафор для писателей
Void writer_enter(){
// мы должны дождаться, пока другие писатели закончат писать
P(writer);
// мы должны удостовериться, что в этот момент нет никаких читалелей
P(reader);
}
Void writer_leave(){
V(reader);
V(writer);
}
Void reader_enter(){
P(writer); // а нет ли внутри писателя?
// критическая секция
P(access);
Rd++;
If(rd == 1) P(reader); // теперь писатель будет знать, что кто-то читает
V(access);
V(writer);
}
Void reader_leave ( ) {
P(access);
Rd--;
If(rd == 0) V(reader); // теперь писатель будет знать, что никто больше не читает
V(access);
}
[править] Задача 5
Какого размера должен быть квант информации, чтобы минимизировать время передачи в конвейере?
Можно выписать общую формулу. Пусть P - длина пути, L - исходная длина сообщения, N - длина единичного куска, на который мы бьем сообщения.
Тогда время передачи будет равно: 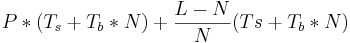 . Первая часть - время прохода первого куска (разгон конвейера), вторая - время передачи остальных кусков. По сути - если мы бьем на очень мелкие куски, то слишком часто будет запускаться процесс передачи и очень часто будет возникать Ts, если очень большие куски - очень большой множитель будет перед Tb. Дифференцированием по N находим оптимум. Не забываем при этом, что исходное выражение можно таким образом пустить по двум путям (или больше) и разбивать уже нужно тогда не L, а
. Первая часть - время прохода первого куска (разгон конвейера), вторая - время передачи остальных кусков. По сути - если мы бьем на очень мелкие куски, то слишком часто будет запускаться процесс передачи и очень часто будет возникать Ts, если очень большие куски - очень большой множитель будет перед Tb. Дифференцированием по N находим оптимум. Не забываем при этом, что исходное выражение можно таким образом пустить по двум путям (или больше) и разбивать уже нужно тогда не L, а 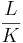 , где K - число непересекающихся путей.
, где K - число непересекающихся путей.
[править] Ссылки
- Реализация считающих семафоров с помощью двоичных
- Алгоритм Деккера и модели консистентности памяти
- мануал по MPI