МФСП, 02 семинар (от 08 сентября)
Материал из eSyr's wiki.
| (3 промежуточные версии не показаны) | |||
| Строка 1: | Строка 1: | ||
| - | Цель этих | + | Цель этих 4—5 занятий будет рассказать оcновы RSL. |
| - | + | Практическое задание: Необходимо будет по задаче написать явную-неявную спецификацию, тестовое покрытие, тестовый драйвер и реализацию на С++, удовлетворяющую спецификации. | |
Типы данных в RSL: | Типы данных в RSL: | ||
| Строка 7: | Строка 7: | ||
* Int +, −, ×, /, \, ↑, abs, real | * Int +, −, ×, /, \, ↑, abs, real | ||
* Nat {|I=Int, i > 0|} | * Nat {|I=Int, i > 0|} | ||
| - | * Real. | + | * Real. Всегда должны присутствовать точка и одна цифра после точки. +, −, ×, /, abs, int (сиречь trunc) |
* Char 'A'...'Z' | * Char 'A'...'Z' | ||
* Text — посл. символов | * Text — посл. символов | ||
| - | * Unit. | + | * Unit. Единственное значение, использующееся для функций без параметров |
== Логика в RSL == | == Логика в RSL == | ||
| - | Трёхзначная, | + | Трёхзначная, помимо true/false есть ещё chaos (ошибка, нетипизированное). |
| - | Все таблицы ит. | + | Все таблицы ит. строятся из того, что в RSL ленивые вычисления логических выражений, крме того ~chaos = chaos. |
(по гор. второй операнд, по верт. — первый) | (по гор. второй операнд, по верт. — первый) | ||
| Строка 132: | Строка 132: | ||
</td></tr></table> | </td></tr></table> | ||
| - | Для описания альтернатив | + | Для описания альтернатив используется if-then-else: |
'''if''' expr1 '''then''' expr2 '''else''' expr3 '''end''' | '''if''' expr1 '''then''' expr2 '''else''' expr3 '''end''' | ||
| Строка 146: | Строка 146: | ||
'''if''' a '''then''' expr2 '''else''' expr3 '''end''' = expr2 = '''if''' a '''then''' expr2 [<math>\frac{true}{a}</math>]'''else''' expr3[false/a] '''end''' = expr2 | '''if''' a '''then''' expr2 '''else''' expr3 '''end''' = expr2 = '''if''' a '''then''' expr2 [<math>\frac{true}{a}</math>]'''else''' expr3[false/a] '''end''' = expr2 | ||
| - | В RSL, как и в | + | В RSL, как и в обычном матлоге, используются кванторы ∃, ∀, !∃. |
| - | Задачи. Будут | + | Задачи. Будут выписываться тождества обычной логики, нужно проверить, работает ли оно в RSL: |
| - | ~~a ≡ a — | + | ~~a ≡ a — выполняется |
true or a ≡ true — выполняется | true or a ≡ true — выполняется | ||
| Строка 213: | Строка 213: | ||
∀ i: Int • ∃ j: Int • i+j=0 — истина (при j = -i) | ∀ i: Int • ∃ j: Int • i+j=0 — истина (при j = -i) | ||
| - | ∀ i: Int • ∃ j: Nat • i+j=0 — не удовл (нельзя найти j для | + | ∀ i: Int • ∃ j: Nat • i+j=0 — не удовл (нельзя найти j для положительного i) |
∃ i: Int • ∀ j: Int • i+j=0 — не верно | ∃ i: Int • ∀ j: Int • i+j=0 — не верно | ||
| - | Написать на RSL выражение, | + | Написать на RSL выражение, выражающее тот факт, что нет наиболее целого числа: |
~(∃ i: Int • ∀ j: Int; • (i >= j ≡ true)) | ~(∃ i: Int • ∀ j: Int; • (i >= j ≡ true)) | ||
| Строка 225: | Строка 225: | ||
== Описание функций в RSL == | == Описание функций в RSL == | ||
| - | Прежде чем узнать описание функций, | + | Прежде чем узнать описание функций, узнаем, что такое декартово произведение типов: |
Type1 × Type2 × ... × Typen | Type1 × Type2 × ... × Typen | ||
| Строка 231: | Строка 231: | ||
(5, "ABC", true): Intx × Text × Bool | (5, "ABC", true): Intx × Text × Bool | ||
| - | Для декартовых | + | Для декартовых произведений определено только равенство и неравенство |
| - | + | Константы в RSL — частный случай функций (функции без аргументов). Функции могут задаваться: | |
| - | * Явно. | + | * Явно. описание, как вычисляется, или знач. |
| - | * Неявно. | + | * Неявно. Накладываются условия на значения. |
| - | * Аксиоматически. Опис., | + | * Аксиоматически. Опис., … |
Константы: | Константы: | ||
| Строка 243: | Строка 243: | ||
Явное задание: | Явное задание: | ||
| - | name: Type = val #задание | + | name: Type = val #задание значения |
Пример: x : Int = 5 | Пример: x : Int = 5 | ||
| Строка 251: | Строка 251: | ||
x : Int • x > 0 | x : Int • x > 0 | ||
| - | Аксиоматически: | + | Аксиоматически: можно использовать оба варианта |
В разделе опис. констант: x: Int | В разделе опис. констант: x: Int | ||
| - | В | + | В разделе опис. аксиом: |
'''Axiom''' | '''Axiom''' | ||
x ≡ 1 или например | x ≡ 1 или например | ||
| Строка 259: | Строка 259: | ||
Функции в RSL: | Функции в RSL: | ||
| - | * Всюду | + | * Всюду вычислимые. Для любого x из области предусловия существует единственное y, таке что f(x) = y^ |
∀ x: T1 • !∃ y : T2 • f(x)=y | ∀ x: T1 • !∃ y : T2 • f(x)=y | ||
| - | * Частично | + | * Частично вычислимые. Для некоторых значений x могут иметь 0, 2 или более значений |
'''value''' | '''value''' | ||
name : Type → result_Type | name : Type → result_Type | ||
| - | для | + | для частично вычислимых — стрелочка с тильдой. В случае сложных типов используется декартово произведение |
Явная спецификация: | Явная спецификация: | ||
| Строка 280: | Строка 280: | ||
'''value''' | '''value''' | ||
f : Int → Int; | f : Int → Int; | ||
| - | f(x) as r | + | f(x) as r /* определение новой переменной, связанной с значением функции */ |
| - | post r>x | + | post r>x /* постусловие, связывающее аргументы и значения функции */ |
| - | Пример | + | Пример описания квадратного корня: |
sqrt : Real трелочка с тильдой Real | sqrt : Real трелочка с тильдой Real | ||
sqrt(x) as s | sqrt(x) as s | ||
| Строка 295: | Строка 295: | ||
∀x"Int • f(x) ≡ x | ∀x"Int • f(x) ≡ x | ||
| - | Пример с sqrt: для | + | Пример с sqrt: для частично вычислимой функции предусловие переносится в начало импликации. |
'''value''' | '''value''' | ||
sqrt : Real трелочка с тильдой Real | sqrt : Real трелочка с тильдой Real | ||
| Строка 319: | Строка 319: | ||
cmplx_mul((xr, xi), (yr, yi)) ≡ (xr×yr-xi×yi, xi×yr+xr×yi) | cmplx_mul((xr, xi), (yr, yi)) ≡ (xr×yr-xi×yi, xi×yr+xr×yi) | ||
| - | Функция, | + | Функция, возвращающая некое комплексное число, отличное от заданного |
'''value''' | '''value''' | ||
cmplx_another : complex → complex | cmplx_another : complex → complex | ||
Текущая версия
Цель этих 4—5 занятий будет рассказать оcновы RSL.
Практическое задание: Необходимо будет по задаче написать явную-неявную спецификацию, тестовое покрытие, тестовый драйвер и реализацию на С++, удовлетворяющую спецификации.
Типы данных в RSL:
- Тип данных bool, знчения true, false, операции: ∧, ∨, ~, ⇒, =, ≠
- Int +, −, ×, /, \, ↑, abs, real
- Nat {|I=Int, i > 0|}
- Real. Всегда должны присутствовать точка и одна цифра после точки. +, −, ×, /, abs, int (сиречь trunc)
- Char 'A'...'Z'
- Text — посл. символов
- Unit. Единственное значение, использующееся для функций без параметров
[править] Логика в RSL
Трёхзначная, помимо true/false есть ещё chaos (ошибка, нетипизированное).
Все таблицы ит. строятся из того, что в RSL ленивые вычисления логических выражений, крме того ~chaos = chaos.
(по гор. второй операнд, по верт. — первый)
|
|
|
|
|
Для описания альтернатив используется if-then-else:
if expr1 then expr2 else expr3 end
Как вычисляется:
if true then expr2 else expr3 end = expr2
if false then expr2 else expr3 end = expr3
if chaos then expr2 else expr3 end = chaos
if a then expr2 else expr3 end = expr2 = if a then expr2 [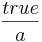 ]else expr3[false/a] end = expr2
]else expr3[false/a] end = expr2
В RSL, как и в обычном матлоге, используются кванторы ∃, ∀, !∃.
Задачи. Будут выписываться тождества обычной логики, нужно проверить, работает ли оно в RSL:
~~a ≡ a — выполняется
true or a ≡ true — выполняется
a or true ≡ true — не выполняется (если подставить chaos)
a => true ≡ true — не выполняется
a => b ≡ ~a or b
a => b ≡ ~a or b T F C
T T T T
F T T T
C T T T
— выполняетя
a or ~a ≡ true — не выполняется
a and ~a ≡ false — не выполняется
a and b and c ≡ a and (b and c)
a = chaos: chaos ≡ chaos = true
a = false: false ≡ false = true
a = true: b = chaos: chaos ≡ chaos = true
b = false: false ≡ false = true
b = true: c ≡ c = true
— выполняется
a or b or c ≡ a or (b or c)
a = chaos: chaos ≡ chaos = true
a = true: truee ≡ true = true
a = false: b = chaos: chaos ≡ chaos = true
b = true: true ≡ true = true
b = false: c ≡ c = true
— выполняется
(a=a)≡true — не выполняется
(a≡a)≡true — выполняется
Чему равно значение выражения:
if true then false else chaos end = true
if a then ~a≡chaos else false end
a expr T T F F C C
= a
if a then ~a=chaos else false end
a expr T C F F C C
Являются ли истиной лед. выражения:
∀ i: Int • ∃ j: Int • i+j=0 — истина (при j = -i)
∀ i: Int • ∃ j: Nat • i+j=0 — не удовл (нельзя найти j для положительного i)
∃ i: Int • ∀ j: Int • i+j=0 — не верно
Написать на RSL выражение, выражающее тот факт, что нет наиболее целого числа:
~(∃ i: Int • ∀ j: Int; • (i >= j ≡ true))
∀ i: Int • ∃ j: Int; • (i >= j ≡ true)
[править] Описание функций в RSL
Прежде чем узнать описание функций, узнаем, что такое декартово произведение типов:
Type1 × Type2 × ... × Typen
(5, "ABC", true): Intx × Text × Bool
Для декартовых произведений определено только равенство и неравенство
Константы в RSL — частный случай функций (функции без аргументов). Функции могут задаваться:
- Явно. описание, как вычисляется, или знач.
- Неявно. Накладываются условия на значения.
- Аксиоматически. Опис., …
Константы:
value name : Type
Явное задание:
name: Type = val #задание значения
Пример: x : Int = 5
Неявно:
name : Type • cond x : Int • x > 0
Аксиоматически: можно использовать оба варианта
В разделе опис. констант: x: Int В разделе опис. аксиом: Axiom x ≡ 1 или например x > 0
Функции в RSL:
- Всюду вычислимые. Для любого x из области предусловия существует единственное y, таке что f(x) = y^
∀ x: T1 • !∃ y : T2 • f(x)=y
- Частично вычислимые. Для некоторых значений x могут иметь 0, 2 или более значений
value name : Type → result_Type
для частично вычислимых — стрелочка с тильдой. В случае сложных типов используется декартово произведение
Явная спецификация:
value f : Int → Int; f(x) = x + 1
p : Real стрелочка с тильдой Real p(x) ≡ 1.0 pre x ≠ 0.0 #условия на аргумент
Неявная спецификация:
value f : Int → Int; f(x) as r /* определение новой переменной, связанной с значением функции */ post r>x /* постусловие, связывающее аргументы и значения функции */
Пример описания квадратного корня:
sqrt : Real трелочка с тильдой Real sqrt(x) as s post ((s×s=x) and (s≥0.0)) pre x≥0.0
Акс. запись:
value f : Int → Int; axiom ∀x"Int • f(x) ≡ x
Пример с sqrt: для частично вычислимой функции предусловие переносится в начало импликации.
value sqrt : Real трелочка с тильдой Real axiom ∀x:Real • x ≥ 0.0 ⇒ ∃s: Real • sqrt(x)=s and s×s=x and s ≥ 0.0
Задачи:
type complex = Real × Real
Определить 0:
value cmplx_zero: complex = (0.0, 0.0)
Функция сложения:
value cmplx_add: complex × complex → complex; cmplx_add((xr, xi), (yr, yi)) ≡ (xr+yr, xi+yi)
Функция умножения:
value cmplx_mul: complex × complex → complex; cmplx_mul((xr, xi), (yr, yi)) ≡ (xr×yr-xi×yi, xi×yr+xr×yi)
Функция, возвращающая некое комплексное число, отличное от заданного
value cmplx_another : complex → complex cmplx_another(x) as a post a ≠ x
Формальная спецификация и верификация программ
|
|


