Определения из теории вероятностей

Материал из eSyr's wiki.

(Различия между версиями)
Перейти к: навигация, поиск
(→Вероятность)
(→Вероятность)
Строка 12: Строка 12:
3. обладает свойством сигма-аддитивности (счетной аддитивности) .
3. обладает свойством сигма-аддитивности (счетной аддитивности) .
 +
 +
= Вероятностное пространство =
 +
==Определение==
 +
 +
'''Вероятностное пространство''' — это тройка <math>(\Omega,\mathcal{F},\mathbb{P})</math>, где
 +
* <math>\Omega \ </math> — это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;
 +
* <math>\mathcal{F}</math> — сигма-алгебра подмножеств <math>\Omega \ </math>, называемых (случайными) событиями;
 +
* <math>\mathbb{P}</math> — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что <math>\mathbb{P}(\Omega) = 1</math>.
 +
 +
=== Замечания ===
 +
* Элементарные события (элементы <math>\Omega \ </math>), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.
 +
* Каждое случайное событие (элемент <math>\mathcal{F}</math>) — это подмножество <math>\Omega \ </math>. Говорят, что в результате эксперимента ''произошло'' случайное событие <math>A\subset \Omega</math>, если (элементарный) исход эксперимента является элементом <math>A</math>.<br>Требование, что <math>\mathcal{F}</math> является сигма-алгеброй подмножеств <math>\Omega \ </math>, позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности [[Дополнение (теория множеств)|дополнения]] любого события.

Версия 11:35, 23 мая 2009

Содержание

Случайный эксперимент

это матетатическая модель соответствующего реального эксперимента, результат которого невозможно точно предсказать.

Случайная величина

Подмножество исходов случайного эксперимента. При многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.

Вероятность

Вероятность (вероятностная мера) — мера достоверности случайного события. Оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента]. Согласно определению П. Лапласа мерой вероятности называется дробь, числитель которой есть число всех благоприятных случаев, а знаменатель - число всех возможных случаев.

Вероятность - мера, заданная на измеримом пространстве (Ω, X): 1. Р(Ω)=1:

2. Р(А)>=0 для любого А€X;

3. обладает свойством сигма-аддитивности (счетной аддитивности) .

Вероятностное пространство

Определение

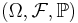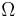Вероятностное пространство — это тройка (\Omega,\mathcal{F},\mathbb{P}), где

  • \Omega \ — это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;
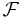  • \mathcal{F} — сигма-алгебра подмножеств 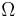\Omega \ , называемых (случайными) событиями;
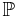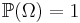  • \mathbb{P} — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что \mathbb{P}(\Omega) = 1.

Замечания

  • Элементарные события (элементы 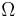\Omega \ ), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.
  • Каждое случайное событие (элемент 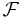\mathcal{F}) — это подмножество 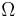\Omega \ . Говорят, что в результате эксперимента произошло случайное событие 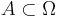A\subset \Omega, если (элементарный) исход эксперимента является элементом A.
    Требование, что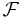 \mathcal{F} является сигма-алгеброй подмножеств 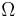\Omega \ , позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.
Получено с http://esyr.name/wiki/%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F_%D0%B8%D0%B7_%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D0%B8_%D0%B2%D0%B5%D1%80%D0%BE%D1%8F%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B5%D0%B9
Личные инструменты
Разделы