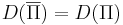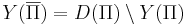Методы Оптимизации, Теормин

Материал из eSyr's wiki.

(Различия между версиями)

Перейти к: навигация, поиск

Версия 05:39, 8 июня 2009

Содержание

1 Введение в теорию сложности
2 Основы линейного программирования
3 Элементы математического программирования
4 Способы решения переборных задач
5 Неотсортировано

Введение в теорию сложности

Индивидуальная и массовая задачи, кодировка задачи, алгоритм решения массовой задачи, временная сложность алгоритма.

Массовая задача $Π$ :

список свободных параметров;
формулировка свойств, которым должно удовлетворять решение задачи.

$Π$ есть множество индивидуальных задач 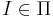$I \in \Pi$ . Индивидуальная задача получается, если всем параметрам присвоить конкретные значения.

Пусть $Σ$ - конечный алфавит, а $Σ *$ - множество слов в этом алфавите. Отображение e: 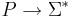$P \rightarrow \Sigma^*$ называется кодировкой задачи П.

Алгоритм $A$ решает массовую задачу $Π$ , если для любой индивидуальной задачи 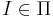$I \in \Pi$ :

$A$ применим к $I$ , то есть останавливается за конечное число шагов
$A$ дает решение $I$

Кодировка задачи P -- такое отобраение 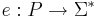$e: P \rightarrow \Sigma^*$ , обладающее следующими свойствами:

Возможность однозначно декодировать, то есть у двух различных ИЗ не может быть одинаковых кодировок.
$e, e - 1$ -- полиномиально вычислимы
Кодировка не избыточна, то есть для любой другой кодировки $e 1$ , удовлетворяющей 1 и 2 условиям справедливо:

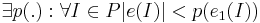
$\exists p(.): \forall I \in P |e(I)| < p(e_{1}(I))$

Язык массовой задачи -- это множество правильных слов, то есть слов, соответствующих ИЗ, имеющим положительный ответ(подразумевается задача распознавания): 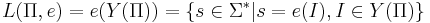$L(\Pi, e) = e(Y(\Pi)) = \{s \in \Sigma^*| s = e(I), I \in Y(\Pi)\}$

Язык алгоритма -- множество слов, принимаемых $A$ , то есть таких, на которых алгоритм останавливается в состоянии $q Y$ , что соответсвует "да": 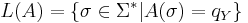$L(A) = \{\sigma \in \Sigma^* | A(\sigma) = q_Y\}$

Алгоритм $A$ решает массовую задачу $Π$ , с кодировкой $e$ , если $L (e,Π) = L (A)$

$t A (s)$ -- число шагов алгоритма $A$ для входа 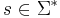$s \in \Sigma^*$ .

Временная сложность 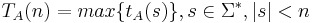$T_{A}(n) = max \{t_{A}(s)\}, s \in \Sigma^*, |s| < n$ .

Задачи распознавания свойств. Классы P и NP.

Задача распознавания свойств -- массовая задача, предполагающая ответ "да" или "нет", в качестве своего решения.

$D (Π)$ -- множество всех возможных значений параметров массовой задачи.
$Y (Π)$ -- множество всех индивидуальных задач, ответом на которые является "да".

Класс полиномиально разрешимых задач (P) -- это такие задачи, временной сложность алгоритма решения которых ограниченна полиномом:

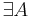$\exists A$ такой, что $A$ решает массовую задачу $Π$ с кодировкой $e$
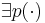$\exists p(\cdot)$ -- полином такой, что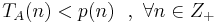 $T_A(n) < p(n)~~,~\forall n \in Z_{+}$

Примеры неполиномиальных задач:

алгоритмически неразрешимые задачи: 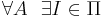такая, что A не применим к I, например,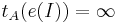
- 10-я проблема Гильберта: по данному многочлену $g$ с целыми коэффициентами выяснить, имеет ли уравнение $g = 0$ целочисленное решение
задачи, для которых длина записи выхода превышает любой наперед заданный полином от длины входа
- найти все маршруты в задаче коммивояжёра

Класс недетерменированно полиномиальных задач (NP) -- это такие задачи, для которых существует алгоритм решения на недерменированной машине Тьюринга:

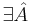$\exists \hat{A}$ для НДМТ такой, что 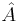$\hat{A}$ решает массовую задачу $Π$ с кодировкой $e$
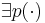$\exists p(\cdot)$ -- полином такой, что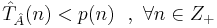 $\hat{T}_{\hat{A}}(n) < p(n)~~,~\forall n \in Z_{+}$

Теорема об экспоненциальной временной оценке для задач из класса NP.

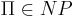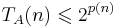Для любой $\Pi \in NP$ существует ДМТ $A$ , решающая ее с не более чем экспоненциальной временной сложностью: $T_A(n) \leqslant 2^{p(n)}$ .

Класс co-NP. Пример задачи, допускающей хорошую характеризацию. Доказательство утверждения о взаимоотношении классов NPC и co-NP.

Дополнительная задача 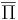$\overline\Pi$ к массовой задаче $Π$ -- задача, получаемая из $Π$ путем введения альтернативного вопроса. То есть если в $Π$ спрашиваем "верно ли $x$ ", то в 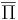$\overline\Pi$ спрашиваем "верно ли, что $\neg x$ "

$D(\overline{\Pi}) = D(\Pi)$
$Y(\overline{\Pi}) = D(\Pi) \setminus Y(\Pi)$

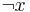Класс $co-P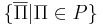$ -- $\{\overline{\Pi} | \Pi \in P\}$

$co-P = P$ .

Класс $co-NP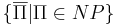$ -- $\{\overline{\Pi} | \Pi \in NP\}$ .

$co-NP = N P$ пока не удалось ни доказать, ни опровергнуть.
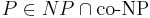
$P \in NP \cap \text{co-NP}$

Массовая задача $Π$ допускает хорошую характеристику, если 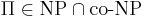$\Pi \in \text{NP} \cap \text{co-NP}$

пример такой задачи -- это задача определения простоты числа.
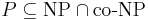
$P \subseteq \text{NP} \cap \text{co-NP}$

Массовая задача $Π'$ с кодировкой $e'$ полиномиально сводится к задаче $Π$ с кодировкой $e$ , если любая индивидуальная задача 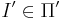$I' \in \Pi'$ может быть сведена за полиномиальное от её длины время к некоторой задаче 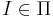$I \in \Pi$ с сохранением ответа.

Массовая задача $Π$ называется NP-полной (универсальной), если

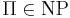
принадлежит классу NP: $\Pi \in \text{NP}$
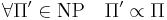
любая задача из NP полиномиально сводится к $Π$ : $\forall \Pi' \in \text{NP} ~~~ \Pi' \propto \Pi$

Класс NPC (NP-complete) -- множество всех NP-полных задач.

Критерий NP-полноты. Д-во NP-полноты задачи ЦЛН

Д-во NP-полноты задачи 3-выполнимость. NP-трудные задачи

Взаимоотношение классов P, NP и NPC, NP и co-NP. Класс PSPACE

Гипотеза. 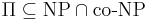$\Pi \subseteq \text{NP} \cap \text{co-NP}$

Гипотеза. Если для некоторой NP-полной задачи $Π$ дополнительная к ней задача 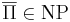$\overline{\Pi} \in \text{NP}$ , то $NP = co-NP$

Класс PSPACE массовых задач -- класс алгоритмов, требующих не более, чем полиномиальной памяти.

Гипотеза. 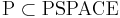$\text{P} \subset \text{PSPACE}$ . При этом NP-полные, NP-трудные, NP-эквивалентные задачи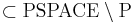 $\subset \text{PSPACE} \setminus \text{P}$

Псевдополиномиальные алгоритмы. Пример для задачи о рюкзаке

Псевдополиномиальный алгоритм - полиномиальный алгоритм, проявляющий экспоненциальный характер только при очень больших значениях числовых параметров.

Пусть $M (I)$ -- некоторая функция, задающая значение числового параметра индивидуальной задачи $I$ . Если таких параметров несколько, в качестве $M (I)$ можно взять или максимальное, или среднее значение, а если задача вовсе не имеет числовых параметров (например, раскраска графа, шахматы и т.п.), то $M (I) = 0$ . Алгоритм называется псевдополиномиальным, если он имеет оценку трудоемкости $T m a x (I) = O (p ( | I | , M (I)))$ , где 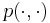$p(\cdot, \cdot)$ -- некоторый полином от двух переменных.

Сильная NP-полнота. Теорема о связи сильной NP-полноты задачи с существованием псевдополиномиального алгоритма ее решения

Полиномиальное сужение массовой задачи $Π$ -- множество таких индивидуальных задач $I$ , числовые параметры которых не превосходят полинома от длины входа: 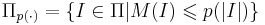$\Pi_{p(\cdot)} = \{ I \in \Pi | M(I) \leqslant p(|I|) \}$

Массовая задача $Π$ называется сильно NP-полной, если её полиномиальное сужение является NP-полным.

задача выполнимости, задача 3-выполнимости -- совпадают со своими полиномиальными сужениями
задача булевых линейных неравенств
задача о целочисленном решении системы линейных уравнений
задача комивояжа

Определение 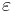$\varepsilon$ -приближенного алгоритма и полностью полиномиальной приближенной схемы (ПППС). Связь между существованием ПППС и псевдополиномиальностью

Теорема об отсутствии ПППС для задач оптимизации, соответствующих сильно NP-полным задачам распознавания

Основы линейного программирования

Определение озЛП. Принцип граничных решений. Алгебраическая и битовая сложность ЛП. Результаты о сложности для задач, близких к ЛП

ЛП (линейное программирование) -- теория, приложения и методы решения системы линейных неравенств с конечным числом неизвестных : 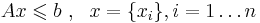$Ax \leqslant b~,~~ x = \{x_{i}\}, i = 1 \dots n$ , существует ли 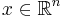$x \in \mathbb{R}^{n}$ , удовлетворяющий данной системе линейных неравентсв

озЛП (основная задача линейного программирования) : найти такой вектор 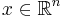$x \in \mathbb{R}^{n}$ -- решение задачи линейного программирования 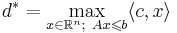$d^{*} = \max_{x \in \mathbb{R}^n;~Ax \leqslant b} \langle c, x \rangle$ , максимизирующее линейную функцию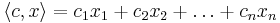 $\langle c, x \rangle = c_1 x_1 + c_2 x_2 + \dots + c_n x_n$

Утверждение (принцип граничных решений). Если озЛП имеет решение, то найдется такая подматрица $A I$ матрицы $A$ , что любое решение системы уравнений $A I x = b I$ реализует максимум $c (x)$ .

Алгебраическая сложность -- количество арифметических операций.

Битовая сложность -- количество операций с битами. Битовая сложность задач ЛП, ЛН полиномиальна.

Вопрос о существовании алгебраически-полиномиального алгоритма для ЛП остается открытым.

Теорема о границах решений задач ЛП с целыми коэффициентами

$Δ(D) = max | det(D 1) |$ , где $D 1$ -- квадратная подматрица $D$

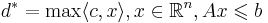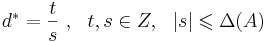
Если задача озЛп $d^{*} = \max\langle c, x\rangle, x \in \mathbb{R}^{n}, Ax \leqslant b$ размерности (n, m) с целыми коэффициентами разрешима, то у нее существует рацональное рашение $x *$ в шаре: $\| x^{*}\| \leqslant \sqrt{n} \Delta([A|b])$ и $d^{*} = \frac{t}{s}~,~~ t,s \in Z,~~|s| \leqslant \Delta(A)$

Теорема о мере несовместности систем линейных неравенств с целыми коэффициентами

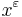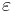$x^{\varepsilon}$ -- $\varepsilon$ -приближенное решение системы ЛН, если

в строчной записи: $\langle a_i , x^{\varepsilon} \rangle \leqslant b_i + \varepsilon~,~~ \forall i \in [1,m]$
в матричной записи: 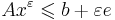$Ax^\varepsilon \leqslant b + \varepsilon e$ , где $e$ -- вектор-столбец из единиц

Теорема. Если система линейных неравенств имеет 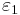$\varepsilon_1$ приближенное решение ( 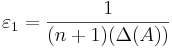$\varepsilon_1 = \frac{1}{(n+1)(\Delta(A))}$ ), то эта система разрешима, то есть имеет точное решение.

Описание метода эллипсоидов

Решает задачу линейного программирования за полиномиальное число шагов.

Суть алгоритма в том, чтобы окружить данный многогранник эллипсоидом, а затем постепенно сжимать этот эллипсоид; оказывается, на каждом этапе объем эллипсоида уменьшается в константное число раз.

Лемма1. Если система 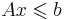$Ax \leqslant b$ совместна,то в шаре $E_0 = \| x \| \leqslant \sqrt{n} \Delta([A|b])$ найдется ее решение.

Таким образом получаем, что если система совместна, то эта лемма позволяет локализовать хотбы бы 1 из ее решений

Введем функцию невязки в точке x -- $t (x) = max i ((A x) i - b i)$ . Точка $x 0 = 0$ -- это центр шара $E 0$ . Если 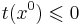$t(x^{0}) \leqslant 0$ , то $x 0$ -- решение. Если это не так, то возмемем s: 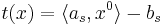$t(x) = \langle a_{s},x^{0}\rangle - b_s$ , значит $x 0$ не удовлетворяет s-ому неравенству системы. Всякий вектор x, удовлетворяющий неравенству s должен лежать в полупространстве 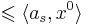$\leqslant \langle a_s, x^{0}\rangle$ . Пересечение этого полупространства с нашей сферой дают полуэлипсоид. Вокруг получившегося полуэлипсоида описываем новую сферу и повторяем алгоритм заново.

Теория двойственности ЛП

Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче.

http://www.mathelp.spb.ru/book1/lprog5.htm

Идея метода Кармаркара

http://logic.pdmi.ras.ru/~yura/modern/02seminar.pdf

Следствия систем линейных неравенств. Афинная лемма Фаркаша (без доказательства)

Определение. 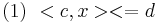$(1)\ <c, x> <= d$ является следствием разрешимой системы ЛН 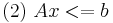$(2)\ Ax <= b$ , если для всех x, для которых выполняется (2), выполняется и (1).

Афинная лемма Фаракша. Линейное неравентсво (1) является следствием разрешимой в вещественный переменных ЛН (2), тогда и только тогда, когда существует 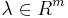$\lambda \in R^{m}$ :

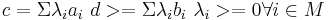
$c = \Sigma\lambda_ia_i\ d >= \Sigma\lambda_ib_i\ \lambda_i >= 0 \forall i \in M\$

http://imcs.dvgu.ru/lib/nurmi/finmath/node41.html

Лемма Фаркаша о неразрешимости

Лемма. Система динейный неравенсив $A x < = b$ неразрешима тогда и только тогда, когда разрешима система:

Невозможно разобрать выражение (неизвестная ошибка): Вставьте сюда формулу

Элементы математического программирования

Способы решения переборных задач

Неотсортировано

Формула градиентного метода в задаче безусловной минимизации
Сведение озЛП к однородной системе уравнений с огрничением x>0
Формула градиентного метода в задаче безусловной минимизации
Формула метода Ньютона в задаче безусловной минимизации
Идея метода штрафов
Геометрическое описание симплекс-метода
Методы глобальной минимизации
Полиномиальный алгоритм округления ?1-приближенного решения системы линейных неравенств
Идея метода эллипсоидов
Идея метода Ньютона
Теорема оптимальности для разложимых функций
Идея метода ветвей и границ. Пример для задачи БЛП
Метод ветвей и границ для ЦЛП. Различные стратегии метода
Метод ветвей и границ для глобальной минимизации Липшицевых функций
Понятие о временной сложности алгоритмов
Понятие о недетерминированно-полиномиальных задачах
Метод динамического программирования для БЛП с неотрицательными коэффициентами
Применение метода динамического программирования для понижения размерности разложимой оптимизационной задачи
Оценка сложности метода эллипсоидов ?2-приближенного решения озЛП

Получено с http://esyr.name/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4%D1%8B_%D0%9E%D0%BF%D1%82%D0%B8%D0%BC%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D0%B8%2C_%D0%A2%D0%B5%D0%BE%D1%80%D0%BC%D0%B8%D0%BD

@@ Строка 179: / Строка 179: @@
 === Лемма Фаркаша о неразрешимости ===
-http://imcs.dvgu.ru/lib/nurmi/finmath/node41.html
+'''Лемма'''.
+Система динейный неравенсив <math>Ax <= b</math> неразрешима тогда и только тогда, когда разрешима система:
+<math>Вставьте сюда формулу</math>
 == Элементы математического программирования ==

Методы Оптимизации, Теормин

Материал из eSyr's wiki.

Версия 05:39, 8 июня 2009

Содержание

Введение в теорию сложности

Индивидуальная и массовая задачи, кодировка задачи, алгоритм решения массовой задачи, временная сложность алгоритма.

Задачи распознавания свойств. Классы P и NP.

Теорема об экспоненциальной временной оценке для задач из класса NP.

Класс co-NP. Пример задачи, допускающей хорошую характеризацию. Доказательство утверждения о взаимоотношении классов NPC и co-NP.

Критерий NP-полноты. Д-во NP-полноты задачи ЦЛН

Д-во NP-полноты задачи 3-выполнимость. NP-трудные задачи

Взаимоотношение классов P, NP и NPC, NP и co-NP. Класс PSPACE

Псевдополиномиальные алгоритмы. Пример для задачи о рюкзаке

Сильная NP-полнота. Теорема о связи сильной NP-полноты задачи с существованием псевдополиномиального алгоритма ее решения

Определение $\varepsilon$ -приближенного алгоритма и полностью полиномиальной приближенной схемы (ПППС). Связь между существованием ПППС и псевдополиномиальностью

Теорема об отсутствии ПППС для задач оптимизации, соответствующих сильно NP-полным задачам распознавания

Основы линейного программирования

Определение озЛП. Принцип граничных решений. Алгебраическая и битовая сложность ЛП. Результаты о сложности для задач, близких к ЛП

Теорема о границах решений задач ЛП с целыми коэффициентами

Теорема о мере несовместности систем линейных неравенств с целыми коэффициентами

Описание метода эллипсоидов

Теория двойственности ЛП

Идея метода Кармаркара

Следствия систем линейных неравенств. Афинная лемма Фаркаша (без доказательства)

Лемма Фаркаша о неразрешимости

Элементы математического программирования

Способы решения переборных задач

Неотсортировано

Просмотры

Личные инструменты

Навигация

инструменты

Разделы

Спецкурсы

9 семестр

7 семестр

5 семестр

3 семестр

Поиск

Инструменты

Методы Оптимизации, Теормин

Материал из eSyr's wiki.

Версия 05:39, 8 июня 2009

Содержание

Введение в теорию сложности

Индивидуальная и массовая задачи, кодировка задачи, алгоритм решения массовой задачи, временная сложность алгоритма.

Задачи распознавания свойств. Классы P и NP.

Теорема об экспоненциальной временной оценке для задач из класса NP.

Класс co-NP. Пример задачи, допускающей хорошую характеризацию. Доказательство утверждения о взаимоотношении классов NPC и co-NP.

Критерий NP-полноты. Д-во NP-полноты задачи ЦЛН

Д-во NP-полноты задачи 3-выполнимость. NP-трудные задачи

Взаимоотношение классов P, NP и NPC, NP и co-NP. Класс PSPACE

Псевдополиномиальные алгоритмы. Пример для задачи о рюкзаке

Сильная NP-полнота. Теорема о связи сильной NP-полноты задачи с существованием псевдополиномиального алгоритма ее решения

Определение -приближенного алгоритма и полностью полиномиальной приближенной схемы (ПППС). Связь между существованием ПППС и псевдополиномиальностью

Теорема об отсутствии ПППС для задач оптимизации, соответствующих сильно NP-полным задачам распознавания

Основы линейного программирования

Определение озЛП. Принцип граничных решений. Алгебраическая и битовая сложность ЛП. Результаты о сложности для задач, близких к ЛП

Теорема о границах решений задач ЛП с целыми коэффициентами

Теорема о мере несовместности систем линейных неравенств с целыми коэффициентами

Описание метода эллипсоидов

Теория двойственности ЛП

Идея метода Кармаркара

Следствия систем линейных неравенств. Афинная лемма Фаркаша (без доказательства)

Лемма Фаркаша о неразрешимости

Элементы математического программирования

Способы решения переборных задач

Неотсортировано

Просмотры

Личные инструменты

Навигация

инструменты

Разделы

Спецкурсы

9 семестр

7 семестр

5 семестр

3 семестр

Поиск

Инструменты

Определение $\varepsilon$ -приближенного алгоритма и полностью полиномиальной приближенной схемы (ПППС). Связь между существованием ПППС и псевдополиномиальностью