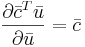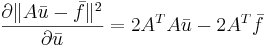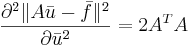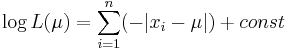МОТП, Задачи на экзамене
Материал из eSyr's wiki.
| Строка 32: | Строка 32: | ||
<math>B\bar{u}=\bar{b}_1u_1+\dots+\bar{b}_nu_n \Rightarrow \frac{\partial B\bar{u}}{\partial u_i}=b_i \Rightarrow \frac{\partial B\bar{u}}{\partial \bar{u}}=B=2A^TA</math> | <math>B\bar{u}=\bar{b}_1u_1+\dots+\bar{b}_nu_n \Rightarrow \frac{\partial B\bar{u}}{\partial u_i}=b_i \Rightarrow \frac{\partial B\bar{u}}{\partial \bar{u}}=B=2A^TA</math> | ||
| + | |||
| + | ==Задача 2. Поиск нормального псевдорешения== | ||
| + | Найти нормальное псевдорешение для системы линейных уравнений. | ||
| + | ===Решение=== | ||
| + | |||
| + | '''В чём суть''': Мы хотим решить несовместную систему линейных уравнений <math>Ax \approx b</math>. Для этого мы будем минимизировать квадрат нормы невязки, т.е найдём <math>x</math> такой, что при нём квадрат нормы невязки будет наименьшим: <math>{\|Ax-b\|}^2\to min_{x}</math>. Теперь по шагам: | ||
| + | |||
| + | 1. Представим норму в матричном виде и раскроем скалярное произведение: | ||
| + | |||
| + | <math>{\|Ax-b\|}^2=\langle Ax-b,Ax-b \rangle = {(Ax-b)}^{T}(Ax-b) = </math> | ||
| + | |||
| + | <math> = {(Ax)}^{T}Ax-b^{T}Ax-{(Ax)}^{T}b+b^{T}b = x^{T}A^{T}Ax-2x^{T}A^{T}b+b^{T}b</math> | ||
| + | |||
| + | 2. Теперь возьмём производную и приравняем её к нулю: | ||
| + | |||
| + | <math>\frac{\partial}{\partial x}(x^{T}A^{T}Ax-2x^{T}A^{T}b+b^{T}b) = 2{A}^{T}Ax - 2{A}^{T}b = 0</math> | ||
| + | |||
| + | 3. Из этого получаем <math>x</math>: | ||
| + | |||
| + | <math>x={({A}^{T}A)}^{-1}{A}^{T}b</math> | ||
| + | |||
==Задача 3. Метод главных компонент (PCA)== | ==Задача 3. Метод главных компонент (PCA)== | ||
Версия 13:20, 26 мая 2010
Математические основы теории прогнозирования
Материалы по курсу
Билеты (2009) | Примеры задач (2009) | Примеры задач контрольной работы (2013) | Определения из теории вероятностей
За нерешение данных задач оценка снижается на балл. — Д. П. Ветров
Задача 1. Вывод формул для векторного дифференцирования
Вывести (считаем все матрицы вещественными):
Решение
Формула 1
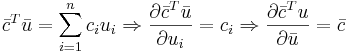
Формула 2
Далее через 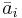 всюду обозначен столбец матрицы A с номером i.
всюду обозначен столбец матрицы A с номером i.
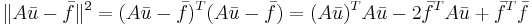
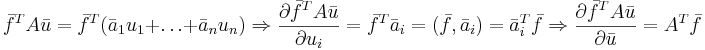
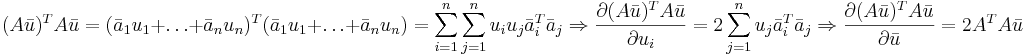
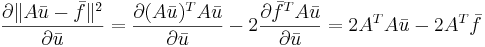
Формула 3
Далее через 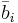 всюду обозначен столбец матрицы B с номером i.
всюду обозначен столбец матрицы B с номером i.
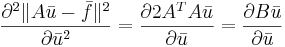
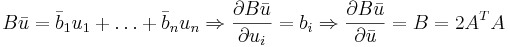
Задача 2. Поиск нормального псевдорешения
Найти нормальное псевдорешение для системы линейных уравнений.
Решение
В чём суть: Мы хотим решить несовместную систему линейных уравнений 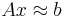 . Для этого мы будем минимизировать квадрат нормы невязки, т.е найдём x такой, что при нём квадрат нормы невязки будет наименьшим:
. Для этого мы будем минимизировать квадрат нормы невязки, т.е найдём x такой, что при нём квадрат нормы невязки будет наименьшим: 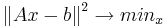 . Теперь по шагам:
. Теперь по шагам:
1. Представим норму в матричном виде и раскроем скалярное произведение:
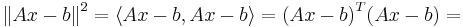
= (Ax)TAx − bTAx − (Ax)Tb + bTb = xTATAx − 2xTATb + bTb
2. Теперь возьмём производную и приравняем её к нулю:
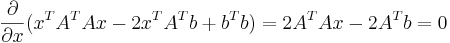
3. Из этого получаем x:
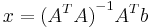
Задача 3. Метод главных компонент (PCA)
Даны р точек в двухмерном пространстве. Найти методом главных компонент первую главную компоненту.
Решение
Рассмотрим следующую задачу: p = 5, x1 = (1,1), x2 = (1,2), x3 = (3,2), x4 = (4,1), x5 = (6,4).
Находим 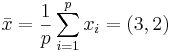 .
.
Находим 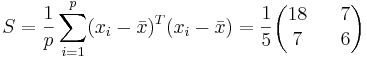
Решаем 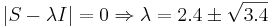 .
.
Находим собственный вектор, соответствующий 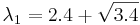 , решая
, решая 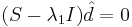 . Получаем
. Получаем 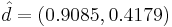 — собственный вектор, соответствующий максимальному собственному значению матрицы ковариации. Он и будет являться первой главной компонентой.
— собственный вектор, соответствующий максимальному собственному значению матрицы ковариации. Он и будет являться первой главной компонентой.
Задача 4. Метод максимального правдоподобия (ММП)
Как метко заметил Оверрайдер, будут задачки на поиск оценки максимального правдоподобия. Не сложные, но чтобы было интереснее, не с нормальным распределением. Что-нибудь типа найти оценку МП на параметр распределения Лапласа.
Решение
Плотность распределения Лапласа: 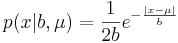 , μ - сдвиг, b - масштаб (подробнее в википедии).
, μ - сдвиг, b - масштаб (подробнее в википедии).
Вариант 1: неизвестный сдвиг, единичный масштаб
Пусть есть распределение Лапласа с неизвестным матожиданием и единичным параметром масштаба. Дана выборка, взятая из этого распределения: 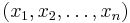 . Оценим параметр μ.
. Оценим параметр μ.
Функция распределения запишется так: 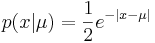
Функция правдоподобия: 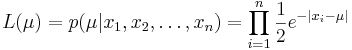
Покажем, что эта функция достигает максимума в точке 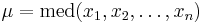 -- когда параметр равен медиане выборки.
-- когда параметр равен медиане выборки.
Упорядочим выборку по возрастанию. Пусть теперь она выглядит так: 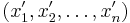 . Рассмотрим последнюю функцию на интервалах вида
. Рассмотрим последнюю функцию на интервалах вида 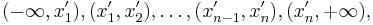 . На первом из них все функции под знаком суммы возрастают, итоговая производная равна n, на втором -- одна убывает, остальные возрастают, производная равна (n-2), и т.д. Переломный момент наступает в середине -- в одной точке перегиба (если n нечётно), или на центральном интервале производная равна 0 (если n чётно). После этого функция только убывает. Там и достигается максимум правдоподобия. Короче, нужно нарисовать график, и всё будет понятно: максимум правдоподобия достигается в точке, равной медиане выборки.
. На первом из них все функции под знаком суммы возрастают, итоговая производная равна n, на втором -- одна убывает, остальные возрастают, производная равна (n-2), и т.д. Переломный момент наступает в середине -- в одной точке перегиба (если n нечётно), или на центральном интервале производная равна 0 (если n чётно). После этого функция только убывает. Там и достигается максимум правдоподобия. Короче, нужно нарисовать график, и всё будет понятно: максимум правдоподобия достигается в точке, равной медиане выборки.
Вариант 2: нулевой сдвиг, неизвестный масштаб
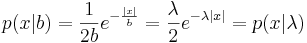
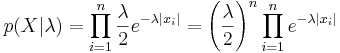
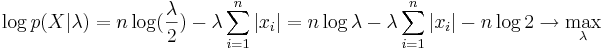
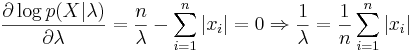
Задача 5. Линейная регрессия
Даны 3-4 точки в двухмерном пространстве - одна координата, это х, другая - t. Задача построить по ним линейную регрессию вида 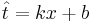 , т.е. найти коэффициенты k и b.
, т.е. найти коэффициенты k и b.
Решение
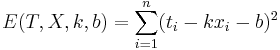
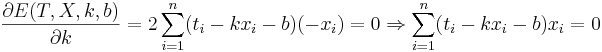
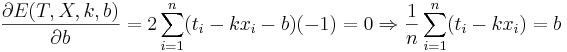
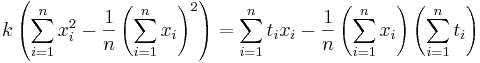
Подставляем значения для xi и ti, получаем k, затем b. Решение проверено на нескольких наборах данных в MATLAB.
Еще один вариант - посчитать напрямую (k,b) = (XTX) − 1XTY, где X - матрица, первый столбец которой составлен из xi, второй - из единиц, а Y - столбец из ti.
Задача 6. Правило множителей Лангранжа
Обязательно кому-то дам задачку на условную максимизацию квадратичной функции с линейным ограничением в виде равенства. Писанины там немного, но вот без правила множителей Лагранжа обойтись вряд ли удастся.
Решение
Пусть нам необходимо максимизировать функцию f(x,y) = − 5x2 + 2xy − 3y2 при условии x − y + 1 = 0.
Запишем функцию Лагранжа 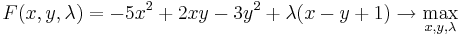 .
.
Приравняем частные производные к нулю:
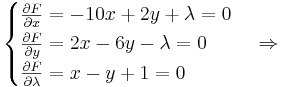
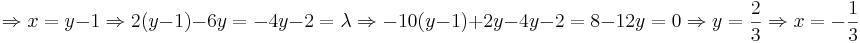 .
.
(По-моему, гораздо проще без функции Лагранжа: y = x + 1;f(x) = − 6x2 − 4x − 3;x = − b / 2a = − 4 / 12 = − 1 / 3)
Задача 10.
Решение
g - гамма, a - альфа, b - бета. Очевидно, выборка из наблюдений дискретной случайно величины со следующим распределением:
1 с вероятностью ga
2 с вероятностью g(1-a)+(1-g)(1-b)
3 с вероятностью b(1-g)
Первый шаг. С учетом начального приближения, вероятности 1, 2 и 3 - 0.25, 0.5 и 0.25 соответственно.
Распределения скрытой компоненты очевидны:
Если текущий элемент выборки 1, то Z=0 с вероятностью 1
Если текущий элемент выборки 3, то Z=1 с вероятностью 1
Если текущий элемент выборки 2, то Z=0 и 1 с вероятностями по 0.5
Учитывая данные в задаче числа, показывающие количество единиц, двоек и троек, получаем, что нужно максимизировать следующую функцию:
30 * log(g * a) + 60 * log(b * (1 − g)) + 20 * (0.5 * log(g * (1 − a)) + 0.5 * log((1 − g) * (1 − b)))
Для поиска максимума нужно взять производные по a, b, g приравнять их к нулю. После первой итерации получаем новые значения:
a=3/4
b=6/7
g=4/11
Второй шаг. С учетом нового начального приближения, вероятности 1, 2 и 3 - 3/11, 2/11 и 6/11 соответственно.
Распределения скрытой компоненты рассчитываются аналогично, для X=1 и 3 отличий нет, для X=2 формула новая, но значения вероятностей тоже совпадают с первым шагом:
P(Z=0)=g*(1-a) / (2/11) = (4/11 * 1/4) / (2/11) = 1/2
Таким образом, функция для оптимизации будет такая же, как на предыдущем шаге. Алгоритм сошелся за два шага.
Ответ:
a=3/4
b=6/7
g=4/11
Задача 11.
Решение
P(a=0) = 0.6 ; P(b=0) = 0.592 ; P(a=0 & b=0) = 0.336
Вероятности получены сложение значений вероятностей всех комбинаций, где выполняется условие. Если бы a и b были независимы, то по определению, третья вероятность была бы произведением первых двух, но это не так, поэтому a и b не независимы.
Однако a и b независимы при с=0:
P(a=0 | c=0) = P(a=0 & c=0)/P(c=0) = 0.5 (определение условной вероятности) P(b=0 | c=0) = 0.8 P(a=0 & b=0 | c=0) = P(a=0 & b=0 & c=0)/P(c=0) = 0.4 = P(a=0 | c=0) * P(b=0 | c=0)
Все остальные соотношения проверяются аналогично.
Задача 13.
Решение
all.pdf, страницы 168-169.
Оценка МП %pi - значение первой скрытой переменной, оно нам дано, поэтому вероятность P(t11 = 1) = 1,P(t12 = 1) = 0.
Оценка МП для матрицы A записана на странице 169. Содержательно эта формула означает следующее. Элемент A[i,j] - вероятность прехода из состояния i в состояние j. Оценка МП - отношение количества известных нам переходов из i в j к количеству раз, которые наблюдали систему в состоянии i. В данной задаче мы наблюдали состояние 1 100 раз, состояние 2 - 99 раз (последний раз не считается). Переход 1->2 наблюдали 25 раз, переход 1->1 - 75 раз, переход 2->1 - 24 раза, переход 2->2 - 75 раз.
Итого матрица A:
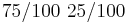
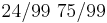
Задача 14. Алгоритм Витерби
Программа на python, решающая задачу (алгоритм взят из [1])
# Helps visualize the steps of Viterbi.
def print_dptable(V):
print " ",
for i in range(len(V)): print "%7s" % ("%d" % i),
print
for y in V[0].keys():
print "%.5s: " % y,
for t in range(len(V)):
print "%.7s" % ("%f" % V[t][y]),
print
def viterbi(obs, states, start_p, trans_p, emit_p):
V = [{}]
path = {}
# Initialize base cases (t == 0)
for y in states:
V[0][y] = start_p[y] * emit_p[y][obs[0]]
path[y] = [y]
# Run Viterbi for t > 0
for t in range(1,len(obs)):
V.append({})
newpath = {}
for y in states:
(prob, state) = max([(V[t-1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
V[t][y] = prob
newpath[y] = path[state] + [y]
# Don't need to remember the old paths
path = newpath
print_dptable(V)
(prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
return (prob, path[state])
states = ('first', 'second')
observations = ('0', '0', '1', '0', '0', '1', '1')
start_probability = {'first': 0.5, 'second': 0.5}
transition_probability = {
'first' : {'first': 0.9, 'second': 0.1},
'second' : {'first': 0.2, 'second': 0.8},
}
emission_probability = {
'first' : {'0': 0.8, '1': 0.2},
'second' : {'0': 0.2, '1': 0.8},
}
def example():
return viterbi(observations,
states,
start_probability,
transition_probability,
emission_probability)
print example()
Вывод программы:
0 1 2 3 4 5 6
secon: 0.10000 0.01600 0.02304 0.00368 0.00074 0.00215 0.00137
first: 0.40000 0.28800 0.05184 0.03732 0.02687 0.00483 0.00087
(0.0013759414272000007, ['first', 'first', 'first', 'first', 'first', 'second', 'second'])
То есть наиболее вероятная последовательность состояний: 1-1-1-1-1-2-2
Задача 15. Алгоритм вперед-назад
Решение
Описание алгоритма с простыми обозначениями можно прочитать здесь: [2]
Значения "альфы" (первой и второй) на каждом шаге:
1: 0.4 и 0.1
2: 0.304 и 0.024
3: 0.05568 и 0.03968
Значения "беты" на каждом шаге, от третьего к первому:
3: 1 и 1
2: 0.61 и 0.68
1: 0.4664 и 0.1576
Нормировочные константы:
3: 0.09536
2: 0.20176
1: 0.20232
И наконец, маргинальные распределения (гамма нулевое - вероятность того, что система была в состоянии 0):
Для t3: 0 с вероятностью ~0.58
Для t2: 0 с вероятностью ~0.919
Для t1: 0 с вероятностью ~0.922
Математические основы теории прогнозирования
Материалы по курсу
Билеты (2009) | Примеры задач (2009) | Примеры задач контрольной работы (2013) | Определения из теории вероятностей