ГОС
Материал из eSyr's wiki.
(Различия между версиями)
(→Интегралы) |
(→Интегралы) |
||
| Строка 4: | Строка 4: | ||
<math>\int cos^3(x) dx = \int (cos^2(x)cos(x)) dx = \int (1 - sin^2(x)) d(sinx) dx = -\int (sin^2(x)) d(sinx) + \int 1 d(sin(x)) = -\frac{sin^3(x)}{3} + sin(x) + C </math> | <math>\int cos^3(x) dx = \int (cos^2(x)cos(x)) dx = \int (1 - sin^2(x)) d(sinx) dx = -\int (sin^2(x)) d(sinx) + \int 1 d(sin(x)) = -\frac{sin^3(x)}{3} + sin(x) + C </math> | ||
| + | |||
| + | <math>\int (3x + 1)^3 dx = \frac{1}{6} \int (3x + 1)^2d(3x + 1)^2 = \frac{1}{6} \frac{(3x + 1)^4}{2}</math> | ||
== Решение линейного однородного дифференциального уравнения с постоянными коэффициентами == | == Решение линейного однородного дифференциального уравнения с постоянными коэффициентами == | ||
Версия 10:40, 4 июня 2010
Интегралы
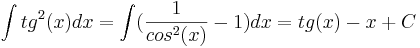
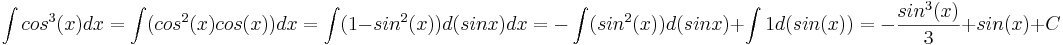
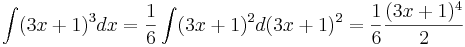
Решение линейного однородного дифференциального уравнения с постоянными коэффициентами
y''' + 2y''' − y' − 2y = 0 (1)
Решение этого уравнения ищется в виде y = eλt
Подставляем этот y в уравнение (1), сокращаем на eλt. Получаем характеристическое уравнение:
λ3 + 2 * λ2 − λ − 2 = 0
Находим корни этого уравнения: λ = 1,λ = 2,λ = − 1
y1 = et,
y2 = e2t,
y3 = e − t
Решение уравнения (1) -- это линейная комбинация yi,i = 1,2,3:
y = C1y1 + C2y2 + C3y3


