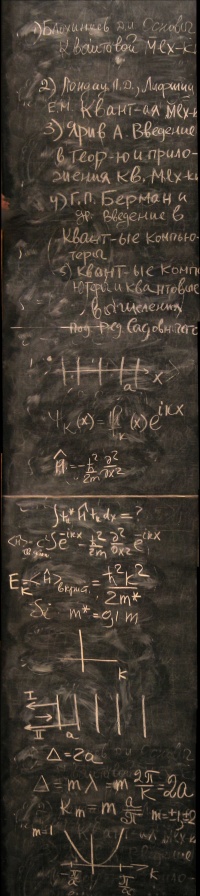ОКФиКВ, 04 лекция (от 05 марта)
Материал из eSyr's wiki.
Диктофонная запись: http://esyr.org/lections/audio/quantphys_2008_summer/QP_08_02_27.ogg
Литература:
- Блохинуев Д. И. Основы квантовой механики
- Ландау Л. Д., Лифшиц Е. М. Квантовая механика
- Ярив А. Введения в теорию и приложения КМ
- Г. П.. Берман и др. Введение в квантовые компьютеры
- Квантовые компьютеры и квантовые вычисления под редакцией Садовничего
Лекция 4.
Продолжаем изучение движ. электрона в период. потенциале. Самый важный тип движения для приложений. И надо интуитивно понять принципы такого движения. С чего же мы начали в прошлый раз: с решения уравнения Ш. для электрона, движущегося в периодическом потенциале. Мы рассмотрели движение в одномерной периодической структуре, а --- период решётки, ось х, движется частица (электрон). И вот что оказывается, ур. Ш. имеет стационарное решение: Ψ_k(x) = f_k(x)e^{ikx}. Важный результат: электрон не рассеивается и движется почти как свободная частица. Отличие в том, что появляется амплитуда.
Рассмотрим характеристики этого движения. Какова энергия: H с домегом = -h/2m δ^2/δx^2 ... .Если попробовать вычислить этот интеграл с функцией Блоха, то так просто не получится, поскольку функция f получается. А что получается: среднее значение энергии в кристале равняется h^2k^2/2m*. Появляется так называемая эфыфективная масса m*, то есть, электрон движется так же, но его масса меняется. Вот масса в таком важном кристалле, как кремний эффективная масса в 10 раз меньше массы электрона свободного.
Построим график. Но так дело обстоит, только если k достаточно мало, но когда k начинает приближаться к определённым значениям, то начинают проявляться особенности в спектре. Вся микроэлектронная промышленность существует потому, что есть эти особенности. Благодаря им появляется новая физика и большое количество приложений. Вспосмним, что рассеиваем электрон как волну, движующуюся в периодическом поле. В таких рассуждениях можно забыть, что есть f, и рассуждать в терминах плоской волны. Что же будет происходить на неоднородностях? Тот, кто изучал волну, скажет, что появляется рассеивание, дифрагирование, дифрагированная волна. Волна пройдёт дальше и отразится от второй плоскости, и появится волна 2. Поскольку всё периодическое, то можно рассмотреть толко этих две волны, остальное наложится. Что происходит с этими дифрагированными волнами? Они интерферируют. Интерференция --- сложение волн. Они складываются. Как складываются? ... Если волны складываются, то конструктивная интерференция, и видно, что для неё волны должны отличаться на челое число периодов. Найдём условия... Рассмотрим случай m = 1 ... Этим решениям соответствует два энергетических уровня. Двум разным функциям соответствует два значения энергии. Теперь лектор рисует результат нашего полукачественного решения: ... Запрещённая зона, зона запрещённых энергий. Есть ещё нижняя зона и верхняя зона запрещённых энергий.В результате волны и ..., несущих исключительно волновой характер, возникают зоны, на зоны делится спекттр. Все современные электроприборы построены на этом эффекте. Почему он важен?
Мы получили зоны, но ведь индекс m пробегает все индексы, соответственно, мы должны поделить в этих точках энергию и сделать аналогичные разрывы. Получили картинку расширенных зон. Но если откроем учебник по физике тврёдого тела, то там используется картина приведённых зон. Картинка приводится к первой зоне. Соотвтетсвенно, у нас есть верхняя зона и нижняя зона.
Первая зона находится на полностью заполненной зоной, зона ... проводимости. ...
Иногда рисуют наьор энергий, запр. зону не рисуют, поотм энергии верхней зоны. Это формальная каритнка. Важный параметр --- ширина запрещённой зоны.
Классификация твёрдых тел
Твёрдые тела подразделяются на металлы, полупровожники и диэлектрики. На самом деле, существуют два класса,металлы и диэл., полупроводники --- подкласс, у которого ширина запрещ. зоны сравнима с энергией светового кванта...
Основы квантовой физики и квантовых вычислений
01 02 03 04 05 06 07 08 09 10 11 12
Календарь
Февраль
| 13 | 20 | 27 | ||
Март
| 05 | 12 | 19 | 26 | |
Апрель
| 02 | 09 | 16 | 23 | 30 |