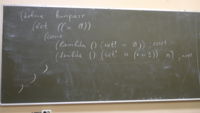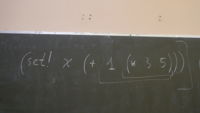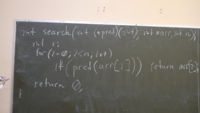Парадигмы программирования, 05 лекция (от 22 октября)
Материал из eSyr's wiki.
Сегодня лектор хотел рассказать про континуации. Это, моэжет быть, не самое зубодробительное, что есть в схеме, но самое интересное. Самым зубодробительным может лектор назвать макросы, потому что он их так и не смог полностью понать.
Континуации вещь в принципе тоже нетривиальная, потому что вещь достаточно новая. В отличие от макросов, которые вроде ни уму, ни сердцу ничего не дают, с конт. наоборот: время потратил, но и когда понимаешь, что это такое ...
Но начёнм не с неё, сначла посмотрим, что можно дедать с помощью лексических замыканий в лиспе. Писать лектор будет на схеме. В частности
- defun в лиспе --- define в схеме. Синтаксис: (defun f (...) ...) -> (define (f ...) ...). Кроме того, define может определять не только функции, но и вещи вроде глоб. переменных. Сами по себе символы ничего не вмещают, для этого надо сказать (define x #f), после чего уже можно сказать (set! x 25). Не все реализ. поддерживают эту хитрость, но она есть.
На самом деле, нам потребуется ещё пара вещей из схемы:
- (map ...) --- то же, что и mapcar в лиспе
- (for_each fun (...)) --- она просто вызывает функцию ради побочного эффекта. Не возвращает ничего.
Свойства лекс. замыканий одинаковы что в схеме, что в лиспе (искл. явл только elisp имени столлмана).
(define funpair
(let ((n 0))
(cons
(lambda () (set! n 0)) ; reset
(lambda () (set! n (+ n 1)) n) ; next
)
)
)
В рез-те вып. этого дела будет нечто хитрое: точечная пара, у которой первый и второй элемент будут функциями. Первая функция — resey, вернуть значение переменной в 0.
Что в результате получилось: с funpair свзяана точечная пара, в car лежит (lambda () (set! n 0)), в cdr — (lambda () (set! n (+ n 1)) n). Теперь лектор берёт интерпретатор, скармливает это и начинает экспериментировать (две скобки потому, что нужно вызывать):
> ((cdr funpair)) 1 > ((cdr funpair)) 2 > ((cdr funpair)) 3
И так далее.
Что это показывает: что лексический контекст (сост. из одной переменной и её значения) не копируется, а сохраняется и остаётся связанным.
> ((car funpair)) > ((cdr funpair)) 1
Получился как будто бы объект с двумя методами. Часто моджет такая штука понадобиться --- часто. Это секвенсер.
Это некий фокус, позв. понять, что такое лекс. контекст.
Обратите внимание, что обе функции связаны с лекс. контекстом, потому что они создавались в нём.
А теперь к теме. Что такое континуация? Это последовательность действий, которые осталось выполнить до завершения вычислений. Вот, у нас есть какие-то вычисления. Наверняка, у нас есть какая-то головная функция (в C main, например). Собственно, всё выч. программы можно представлять как: что осталось сделать до завершения программы. Когда мы в начале выполнения, то нам нужно вызвать эту функцию. после того, когда вызвали, мы вошли в её тело. Что осталось? Осталось вычислить первую форму, вторую, и так до конца. Дальше, допустим, первая форма головной функции это что-нибудь такое:
(set! x (+ 1 (* 3 5))) (...) ...
Что ост. вычислить на след. шаге? Осталось вычислить (+ 1 (* 3 5)), присвоить значений x, и высчисл. след. формы. Дальше мы вошли внутрь (+ 1 (* 3 5)). Что осталось вычислить: (* 3 5), прибавить единицу, присвоить иксу, и всё остальное. Далее: Взять 3, взять 5, умножить, результат прибавить единице, результат присвоить икс, вычилстиь дальше. Дальше у нас элементпрное действие, мы его делаем, получаем 15. Дальше --- тоже элементарное действие, получаем результат 16. Далее, загнать 16 в x. Далее --- вычисл. след. формы.
То есть, при выч. мы желаем элемент. шаги, нам оставался на один шаг меньше, хотя континуация могла становиться больше.
То есть, ещё раз, что такое континуация: это набор всех действ., которые ост. сделать до конца вычислений.
scheme --- один из немногих языков, где континуация явл. объектом первого порядка, то есть с ней можно работать.
В схеме есть функция, хитрая: call-with-current-continuation. Понятно, что программисты люди ленивые, такое они не пишут, поэтому обычно используют call/cc. Как правило, компиляторы и интерпретаторы схемы поддерживают оба имени, но обычно используют второе.
Что эта штука делает: call/cc это штука от одного арг. Этим арг. должна быть функция. Причём, эта функция тоже должна быть функцией от одного аргумента. Что делает call/cc: он вызывает функцию, подав ей в кач. единст. аргумента вот этот объект континуации.
(call/cc f)
Так вот, вызвана будет f, а объектом дадут континуацию. Понятно, что обычно здесь исп. лямбду, но это необязательно.
Как это дело вычисляется: если call/cc выз. f, а f что-то возвращает ( если успеет), то вся эта форма возвр. то, что вернула f. Здесь ничего сверхъест. нет. Но, есть один момент: внутри функции f доступен этот объект, что с ним можно сделать? Его можно вызвать как функцию одного аргумента, и этот вызов приведёт к тому, что форма эта немедленно вернёт управление ровно в том месте, которое было, и в кач. значения вернёт то, что подали континуации как функции одного аргумента, причём это можно сделать после того, как она вернула управление.
Достаточно простая иллюстрация:
> (define store #f)
> (define (f arg) (set! store arg) "simple")
> (let ((x (call/cc f)))
> (write (list x x x))
> )
("simple" "simple" "simple")
Но при этом континуация сохранилась в store.
> (store "complicated")
("complicated" "complicated" "complicated")
Как это реализуется --- по-разному. Есть, например, реализация для C, которая сделана путём сохранения стека.
Вначале лекции летор скзаал, что континуации явл. обобщением многих вещей. Например:
* Досрочное окончание многих функций. (аналог brake/return в C)
Вообще, goto не так и плох, его вполне можно использовать в двух случаях.
- Первый --- cleanup. Например, В начале забирается дин. ресурс, а потом хочется досрочно её завершить. Так вот, не надо дублировать освобождение, нужно сделать goto на cleanup:
- Второй — выход из неск. вложенных циклов. Тут break не поможет. Обычно это делают посредством флага. Не надо так делать. Это второй и последний случай.
Но в совр. языках случаев может быть меньше. В C++ есть деструкторы, в Ada/Java можно именовать for и прочее.
call/cc является обобщением вариантов с доср. выходом из конструкции. Пример: дан предикат от одного аргумента. Дан список из скольких-то элементов. Задача: из этого списка извлечь первый элемент, на котором предикат вернёт истину. Можно ли это сделать с помощью рекурсии? Конечно можно.
(define (search wanted? lst)
(cond
((null? lst) #f)
((wanted? (car lst)) #t)
(#t (search wanted? (cdr lst)))
)
)
В традиции языка scheme — именование предикатов вопр. знаком.
Единственное что — значение глобальных переменных не сохраняется.
Можно так писать? Можно. Но обычно для просмотра вписков хочется исп. мапперы. Можно ли из тут исп.? Можно, но будет не меньше по длине
(define (search wanted? lst)
(call/cc
(lambda (return)
(for-each
(lambda (elem) (if (wanted? elem) (return elem)))
lst
)
#f
)
)
)
Короче ли это? Трудно сказать, строчек больше, но бук примерно столько же. Понятнее ли? Вопрос. Рекурсия привычнее, но на С мы бы написали примерно то же самое:
int search(int (* pred)(int), int * arr, int n)
{
int i;
for (i = 0; i < n; i++)
{
if (pred(arr[i]))
{
return arr[i];
}
}
return 0;
}
Таким обр. мы с помощью call/cc эмулируем выход из циклов. Но возм. на этом не заканчиваются. Что ещё можно: можно заст. прекр. функцию, которая лексически в другом месте. Давайте переделаем функцию search, если у нас не предикат есть, а некая функция. Теперь применим другую парадигму, callback. Мы выбор элемент будем выбирать с помощью функции, которой если элемент понравился, то она будет делать колбэк.
(define (treat elem callback)
(if (wanted? elem) (callback elem))
)
(define (search treat lst)
(call/cc
(lambda (return)
(for-each
(lambda (elem) (treat elem return))
lst
)
#f
)
)
)
Делает то же самое, один момент: функция, которая завершает просмотр, находится в другом месте. Называется это "нелокальный выход".
В явном виде такие вещи есть в языках типа лиспа. В лиспе для этого есть для этого спец. формы, мех. континуаций --- строго более общий, чем мех. нел. выхода.
А вот есть такая вещь, как исключения, они есть во многих языках. Потому, что не смотря на то, что они криво реализованы, сильно облегчают жизнь.
Ошибочно полагать, что парадигма обр. искл. имеет отношение к ООП. Почему так полагают? Потому что впервые с ним сталк. в С++, но сам мех. не имеет отн. к ООП. Что такое ООП: это когда среда исп. прилож. сост. из объектов, они имеют внутр. сост, могут принимать сообщ., как-то менять внутр. сост., обр. к другим объектам, отвечать на сообщ. Как это соотн. к С++, То, что в теории ООП наз. передачей сообщения, в С++ есть вызов методы. И при чём тут обработка искл.? Ни при чём? К какой же парадигме тогджа они ближе? К функциональной. Что есть искл., как не способ альт. завершения фнукции? Если это альт. способ. возвр. из ф-ции, то думать надо не об объектах, а о функциях, а это точно не из ООП понятие. Поэтому, искл. это парадигма, не имеющ. никакого отношения к ООП.
Лектор напомнит, что такое искл:
В качестве обозначение искл. ситуации можно исп. объект почти любого типа, в том числе объект типа Class.
Для возбужд. искл. исп. throw ... . Объекты, не допускающие копирования, нельзя исп.. Как поймать исключение?
Почему из курса арзитектура эвм надо знать, что такое стековый фрейм? Потому что такие вещи, как искл. и хвостовая рекурсия, проще объяснять.
Есть функция из стандартного C++ runtime, __trow_unwind, которая линкуется при исп. искл. Эта функция берёт стековый фрейм и начинает его разматывать, ища обработчик. Если нет, то вызывает деструкторы и схлопывает его. Далее берёт стековый фрейм и так далее. Если дойдёт до вершины стека, то программа завершится.
Можно сымитировать искл. в языках, в окторых нет искл. Например, в С. Там есть setjmp/longjmp.
int setjmp(jmp_buf env);
Принимает setjmp на вход буфер, она туда запис. некуюб инф., которая пригодится для возвр. туда потом. На самом деле, она туда запис. Текущий указатель стека. Возвр. при первом вызове 0.
Когда делается long_jmp(jmp_buf, int), то в след. раз вернёт не 0, а то, что передано.
Единст. ограничение: стековый фрейм должен существовать. Если его уже нет, то "full chaos guaranteered".
Эмуляция искл. с call/cc:
(let ((ret (call/cc ..) ...
Это всё хорошо, но это всё, что нелок. выходы, что искл --- ситуация, когда мы глубже в стеке.
Гораздо интереснее, когда оно уже отработало, стековый фрейм прибился, но call/cc мощнее тем, что он позв. вернуться и в этой ситуации.
Что можно с помощью этого сделать: например, сопрограммы (жутко медленно, но красиво). Что для этого нужно сделать:
(define queue_ '())
(define (empty_queue?) (null? queue))
(define (enqueue x))
(set! queue (append queue (lest x)))
)
(define (deque)
(let ((x (car queue)))
(set! queue (cdr queue))
X
)
)
(define (fork proc) ; процедура, которая некую функцию ставит в очередь
(call/cc (lambda (k) (enqueue k) (proc))) ;в конец процедуры ставим то место той процедуры, которая вызвала fork
)
(define (yield)
(call/cc (lambda (k) (enqueue k) ((dequeue))))
)
(define (thread_exit)
(if (empty_queue?) (exit) ((dequeue)))
)
Есть такой стиль, как continuation past, стиль прогр. с передачей континуаций. Один из языков, который это вроде поддерживает --- Io. Идея такая, что одним из арг. передаются континуации. Стека там нет, там вообще нет возврата. Любопытная штука, бывает и такое.
След. лекция посв. лямбда-исчислению.
Есть книжка Фил, Харрисон, функц. программирование, там оно изложено.
Иллюстрации
Введение в парадигмы программирования
01 02 03 04 05 06 07 08 09 10 11
Календарь
Сентябрь
| 24 | ||||
Октябрь
| 01 | 08 | 15 | 22 | 29 |
Ноябрь
| 05 | 12 | 19 | 26 | |
Декабрь
| 03 |
Экзамен по курсу пройдёт 10 декабря 2009 года в 18:00 в аудитории 524. | Список экзаменационных вопросов