Конструирование Компиляторов, Теоретический минимум (2009)
Материал из eSyr's wiki.
| (35 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
''см. также [[Конструирование Компиляторов, Теоретический минимум|ответы на вопросы теоретического минимума 2007 года]], [[Конструирование Компиляторов, Определения|список определений]].'' | ''см. также [[Конструирование Компиляторов, Теоретический минимум|ответы на вопросы теоретического минимума 2007 года]], [[Конструирование Компиляторов, Определения|список определений]].'' | ||
| + | == Алфавит == | ||
| - | + | Алфавит - конечное множество символов | |
| - | + | ||
| - | # Определение детерминированной машины Тьюринга | + | == Определение грамматики == |
| - | + | Грамматика <math>~G = (N,T,P,S)</math> - четверка множеств, где | |
| - | + | * <math>~N</math> - алфавит нетерминальных символов | |
| - | + | * <math>~T</math> - алфавит терминальных символов, <math>N \cap T = \empty</math>; | |
| - | + | * <math>~P</math> - множество правил вида <math>\alpha \rarr \beta, \alpha \in ( N \cup T)^*N(N \cup T)^*, \beta \in (N \cup T)^*</math> | |
| - | + | * <math>S \in N</math> - начальный символ или аксиома грамматики | |
| - | + | ||
| - | + | == Определение грамматик типа 0 по Хомскому == | |
| - | # Определение праволинейной грамматики | + | Если на грамматику <math>~G = (N, T, P, S)</math> не накладываются никакие ограничения, то её называют грамматикой типа 0, или грамматикой без ограничений. |
| - | + | ||
| - | + | == Определение грамматик типа 1 (неукорачивающих) по Хомскому == | |
| - | + | Если | |
| - | + | # Каждое правило грамматики, кроме <math>S \rarr \epsilon </math> , имеет вид <math>\alpha \rarr \beta, |\alpha| \le |\beta|</math> | |
| - | + | # В том случае, когда <math>S \rarr \epsilon \in P</math>, символ <math>~S</math> не встречается в правых частях правил | |
| - | + | то грамматику называют грамматикой типа 1, или неукорачивающей. | |
| - | + | ||
| - | + | == Грамматика типа 2 (Контекстно-свободная, КС) по Хомскому == | |
| - | + | ||
| - | # Определение функции lastpos для поддерева в дереве регулярного выражения | + | Грамматика типа 2 (Контекстно-свободная, КС) - грамматика, где каждое правило <math>p \in P</math> имеет вид <math>A \rarr \alpha</math>, где <math> A \in N, \alpha \in (N \cup T)^*</math> |
| - | # Определение функции followpos для позиций в дереве регулярного выражения | + | |
| - | + | == Грамматика типа 3 (Праволинейная) по Хомскому == | |
| - | + | ||
| - | + | Грамматика типа 3 (Праволинейная) - грамматика, где <math> \forall p \in P </math> имеет вид либо <math> A \rarr xB </math>, либо <math> A \rarr x </math>, где <math> A,B \in N, x \in T^* </math> | |
| - | + | ||
| - | + | == Определение детерминированной машины Тьюринга == | |
| - | + | '''Детерминированная машина Тьюринга''' — T<sub>m</sub> = (Q, Г, Σ, D, q<sub>0</sub>, F) | |
| - | + | * Q — конечное множество состояний | |
| - | + | * Г — конечное множество ленточных символов (конечный алфавит), один из которых называется пустым и обозначается обычно b | |
| - | + | * Σ — входной алфавит, Σ ⊆ Г\{b} (b - пустой символ) | |
| - | + | * D — правила перехода | |
| - | + | ** D: (Q\F) × Г → Q × Г × {L, R} | |
| - | + | * q<sub>0</sub> ∈ Q — начальное состояние | |
| - | + | * F ⊆ Q — множество конечных состояний | |
| - | # Определение детерминированного МП автомата | + | |
| - | # Определение конфигурации МП автомата | + | |
| - | + | ||
| - | + | == Определение конфигурации машины Тьюринга == | |
| - | + | Конфигурацией машины Тьюринга называется тройка (q, w, i), где | |
| - | + | * q ∈ Q — состояние машины Тьюринга | |
| - | # Определение нормальной формы Хомского для КС-грамматики | + | * w ∈ Г* —текущее содержимое занятого участка ленты, w = a<sub>1</sub> … a<sub>n</sub> |
| - | # Определение правостороннего вывода в КС-грамматике | + | * i ∈ Z — положение головки машины Тьюринга |
| - | + | ||
| - | + | == Определение языка, допускаемого машиной Тьюринга == | |
| - | + | Язык, допускаемый машиной Тьюринга — множество таких слов w, что, машина Тьюринга, находясь в состоянии (q<sub>0</sub>, w, 1) может достигнуть через конечное число переходов состояния q ∈ F. | |
| - | + | ||
| - | + | == Соотношение между языками, порождаемыми грамматиками типа 0 и языками, допускаемыми машинами Тьюринга == | |
| - | + | Класс языков, допускаемых машиной Тьюринга, эквивалентен классу языков, порождаемых грамматиками типа 0. | |
| - | + | ||
| - | + | == Объяснить разницу между недетерминированной и детерминированной машиной Тьюринга == | |
| - | + | Детерминированная машина Тьюринга из данного состояния по данному символу может сделать не более одного перехода, недетерминированная же таким свойством не обладает. | |
| - | + | ||
| - | + | == Определение регулярного множества == | |
| - | + | ||
| - | + | '''Регулярное множество''' в алфавите T определяется следующим образом: | |
| + | * <math> \varnothing </math> — регулярное множество в алфавите T | ||
| + | * <math> ~\{a\} </math> — регулярное множество в алфавите T для каждого a ∈ T | ||
| + | * <math> ~\{\epsilon\} </math> — регулярное множество в алфавите T | ||
| + | * Если P и Q — регулярные множества в алфавите T, то регулярны множества | ||
| + | ** <math>~P \cup Q</math> (объединение) | ||
| + | ** <math>~PQ</math> (конкатенация, <math>\{ pq | p \in P, q \in Q\}</math>) | ||
| + | ** <math>~P^*</math> (итерация: <math>P^* = \{\epsilon\} \cup P \cup PP \cup PPP \cup ...)</math> | ||
| + | * Ничто другое не является регулярным множеством в алфавите T | ||
| + | |||
| + | == Определение регулярного выражения == | ||
| + | '''Регулярное выражение''' — форма записи [[Конструирование Компиляторов, Определения#Регулярное монжество|регулярного множества]]. | ||
| + | |||
| + | Регулярное выражение и обозначаемое им регулярное множество определяются следующим образом: | ||
| + | * ∅ — обозначает множество {} | ||
| + | * ε — обозначает множество {ε} | ||
| + | * ''a'' — обозначает множество {''a''} | ||
| + | * Если РВ ''p'' и ''q'' обозначают множества ''P'' и ''Q'' соответственно, то: | ||
| + | ** (''p''|''q'') обозначает ''P'' ∪ ''Q'' | ||
| + | ** ''pq'' обозначает ''PQ'' | ||
| + | ** (''p''*) обозначет ''P''* | ||
| + | * Ничто другое не является регулярным выражением в данном алфавите | ||
| + | |||
| + | == Определение праволинейной грамматики == | ||
| + | Праволинейная грамматика или грамматика типа 3 по Хомскому — грамматика вида A → w, A → wB, w ∈ T*. | ||
| + | |||
| + | == Определение недетерминированного конечного автомата == | ||
| + | '''Недетерминированный конечный автомат''' - M = (Q, Σ, D, q<sub>0</sub>, F) | ||
| + | * Q — конечное непустое множество состояний | ||
| + | * Σ — входной алфавит | ||
| + | * D — правила перехода | ||
| + | ** Q × ( Σ ∪ {ε} ) → 2<sup>Q</sup> | ||
| + | * q<sub>0</sub> ∈ Q — начальное состояние | ||
| + | * F ⊆ Q — множество конечных состояний | ||
| + | <!-- про epsilon - моя отсебятина, его обычно потом отдельно добавляют --> | ||
| + | <!-- или от нас требуется только нестрогое определение? --> | ||
| + | |||
| + | == Определение детерминированного конечного автомата == | ||
| + | '''Детерминированный конечный автомат''' - M = (Q, Σ, D, q<sub>0</sub>, F) | ||
| + | * Q — конечное непустое множество состояний | ||
| + | * Σ — конечный входной алфавит | ||
| + | * D — правила перехода | ||
| + | ** Q × Σ → Q | ||
| + | * q<sub>0</sub> ∈ Q — начальное состояние | ||
| + | * F ⊆ Q — множество конечных состояний | ||
| + | <!-- или от нас требуется только нестрогое определение? --> | ||
| + | |||
| + | == Объяснить разницу между недетерминированным и детерминированным конечным автоматом == | ||
| + | Недетерминированный конечный автомат является обобщением детерминированного. Существует теорема, гласящая, что «Любой недетерминированный конечный автомат может быть преобразован в детерминированный так, чтобы их языки совпадали» (такие автоматы называются эквивалентными). | ||
| + | В детерменированном автомате из одного состояния допускается не более одного перехода для каждого символа алфавита, в недетерменированном - произвольное количество. Кроме того, в НКА возможны эпсилон-переходы. | ||
| + | |||
| + | == Определение конфигурации конечного автомата == | ||
| + | Пусть ''M'' = (''Q'', ''T'', ''D'', ''q''<sub>0</sub>, ''F'') — НКА. Конфигурацией автомата ''M'' называется пара (''q'', ω) ∈ ''Q'' × ''T''*, где ''q'' — текущее состояние управляющего устройства, а ω — цепочка символов на входной ленте, состоящая из символов под головкой и всех символов справа от неё. | ||
| + | |||
| + | == Определение языка, допускаемого конечным автоматом == | ||
| + | Автомат ''M'' допускает цепочку ω, если (''q''<sub>0</sub>, ω) ⊦* (''q'', ε) для некоторого ''q'' ∈ ''F''. Языком, допускаемым автоматом ''M'', называется множество входных цепочек,допускаемых автоматом ''M''. То есть: | ||
| + | * ''L(M)'' = {ω | ω ∈ ''T''* и (''q''<sub>0</sub>, ω) ⊦* (''q'', ε)'' для некоторого ''q'' ∈ ''F''} | ||
| + | |||
| + | == Определение ε-замыкания для подмножества состояний НКА == | ||
| + | ε-замыкание множества состояний ''R'', ''R'' ⊆ ''Q'' — множество состояний НКА, достижимых из состояний, входящих в ''R'', посредством только переходов по ε, то есть множество | ||
| + | * S = ⋃<sub>q ∈ R</sub> {p | (q, ε) ⊦* (p, ε)} | ||
| + | |||
| + | == Определение расширенной функции переходов для КА == | ||
| + | <!-- не для НКА ли это определение? --> | ||
| + | Расширенная функция переходов множества состояний ''R'', ''R'' ⊆ ''Q'' по ''a'' — множество состояний НКА, в которые есть переход на входе ''a'' для состояний из ''R'', то есть множество | ||
| + | * S = ⋃<sub>q ∈ R</sub> {p | p ∈ D(q, a)} | ||
| + | |||
| + | == Определение расширенной функции переходов для НКА == | ||
| + | == Определение расширенной функции переходов для ДКА == | ||
| + | |||
| + | == Определение функции firstpos для поддерева в дереве регулярного выражения == | ||
| + | Функция ''firstpos(n)'' для каждого узла ''n'' узла синтаксического дерева регулярных выражений даёт множество позиций, которые соответствуют первым символам в цепочках, генерируемых подвыражением с вершиной ''n''. Построение: | ||
| + | {| | ||
| + | !узел ''n'' | ||
| + | !''firstpos(n)'' | ||
| + | |- | ||
| + | |ε | ||
| + | |∅ | ||
| + | |- | ||
| + | |''i'' ≠ ε | ||
| + | |{''i''} | ||
| + | |- | ||
| + | |u | v | ||
| + | |''firstpos''(''u'') ∪ ''firstpos''(''v'') | ||
| + | |- | ||
| + | |u . v | ||
| + | |if ''nullable''(''u'') then ''firstpos''(''u'') ∪ ''firstpos''(''v'') else ''firstpos''(''u'') | ||
| + | |- | ||
| + | |v* | ||
| + | |''firstpos''(''v'') | ||
| + | |} | ||
| + | |||
| + | == Определение функции lastpos для поддерева в дереве регулярного выражения == | ||
| + | Функция ''lastpos(n)'' для каждого узла ''n'' узла синтаксического дерева регулярных выражений даёт множество позиций, которым соответствуют последние символы в цепочках, генерируемых подвыражениями с вершиной ''n''. | ||
| + | Построение ''lastpos''(''n''): | ||
| + | {| | ||
| + | !узел ''n'' | ||
| + | !''lastpos(n)'' | ||
| + | |- | ||
| + | |ε | ||
| + | |∅ | ||
| + | |- | ||
| + | |''i'' ≠ ε | ||
| + | |{''i''} | ||
| + | |- | ||
| + | |u | v | ||
| + | |''lastpos''(''u'') ∪ ''lastpos''(''v'') | ||
| + | |- | ||
| + | |u . v | ||
| + | |if ''nullable''(''v'') then ''lastpos''(''u'') ∪ ''lastpos''(''v'') else ''lastpos''(''v'') | ||
| + | |- | ||
| + | |v* | ||
| + | |''lastpos''(''v'') | ||
| + | |} | ||
| + | |||
| + | == Определение функции followpos для позиций в дереве регулярного выражения == | ||
| + | Функция ''followpos(i)'' для позиции ''i'' есть множество позиций ''j'' таких, что существует некоторая строка ''…cd…'', входящая в язык, описываемый регулярным выражением, такая, что позиция ''i'' соответствует вхождению ''c'', а позиция ''j'' — вхождению ''d''. | ||
| + | |||
| + | == Сформулировать соотношение между регулярными множествами и языками, допускаемыми КА == | ||
| + | Любой конечный автомат распознает регулярное множество цепочек символов входного алфавита. | ||
| + | Верно и обратное — для любого регулярного языка можно построить распознающий его конечный автомат. | ||
| + | |||
| + | == Определение регулярной грамматики == | ||
| + | Регулярные грамматики — праволинейные (A → w, A → wB, w ∈ T*), леволинейные (A → w, A → Bw, w ∈ T*). | ||
| + | |||
| + | == Сформулировать соотношение между языками, порождаемыми праволинейными грамматиками и языками, допускаемыми КА == | ||
| + | Для любой праволинейной грамматики существует конечный автомат, проверяющий порождаемый грамматикой язык. Для любого конечного автомата существует праволинейная грамматика, порождающая проверяемый конечным автоматом язык. | ||
| + | |||
| + | == Определение эквивалентных состояний ДКА == | ||
| + | Два состояния <math>q_i</math> и <math>q_j</math> называются эквивалентными (<math>q_i</math> ~ <math>q_j</math>), если <math>\forall z\in</math> T* верно, что <math>D(q_i, z)\in T \Leftrightarrow D(q_j, z)\in T</math> | ||
| + | |||
| + | == Определение различимых состояний ДКА == | ||
| + | |||
| + | == Определение контекстно-свободной грамматики без ε-правил == | ||
| + | * A → α, α ∈ (N ∪ T)<sup>+</sup> | ||
| + | * допускается S → ε, если S не входит ни в какую правую часть | ||
| + | |||
| + | == Определение контекстно-свободной грамматики == | ||
| + | A → α, α ∈ (N ∪ T)* | ||
| + | |||
| + | == Определение выводимости в грамматике == | ||
| + | Определим на множестве (''N'' ∪ ''T'')* грамматики ''G'' = (''N'', ''T'', ''P'', ''S'') бинарное отношение выводимости «⇒» следующим образом: если ''δ'' → ''γ'' ∈ ''P'', то ''αδβ'' ⇒ ''αγβ'' для всех ''α'', ''β'' ∈ (''N'' ∪ ''T'')*. Если ''α''<sub>1</sub> ⇒ ''α''<sub>2</sub>, то ''α''<sub>2</sub> непосредственно выводима из ''α''<sub>1</sub>. | ||
| + | |||
| + | Если ''α'' ⇒<sup>''k''</sup> ''β'' (''k'' ≥ 0), то существует последовательность шагов | ||
| + | * ''γ''<sub>0</sub> ⇒ ''γ''<sub>1</sub> ⇒ ''γ''<sub>2</sub> ⇒ … ⇒ ''γ''<sub>''k'' − 1</sub> ⇒ ''γ''<sub>''k''</sub> | ||
| + | где ''α'' = ''γ''<sub>0</sub> и ''β'' = ''γ''<sub>''k''</sub>. Последовательность цепочек ''γ''<sub>0</sub>, ''γ''<sub>1</sub>, ''γ''<sub>2</sub>, …, ''γ''<sub>''k'' − 1</sub>, ''γ''<sub>''k''</sub> в этом случае называется выводом ''β'' из ''α''. | ||
| + | |||
| + | == Определение языка, порождаемого КС-грамматикой == | ||
| + | Языком, порождаемым грамматикой ''G'' = (''N'', ''T'', ''P'', ''S'') (обозначается ''L''(''G'')) называется множество всех цепочек терминалов, выводимых из аксиомы, то есть: | ||
| + | * ''L''(''G'') = {''w'' | ''w'' ∈ ''T''*, ''S'' ⇒<sup>+</sup> ''w''} | ||
| + | |||
| + | == Определение сентенциальной формы == | ||
| + | '''Сентенциальная форма''' — цепочка над алфавитом <math> (T \cup N)^* </math>, выводимая из аксиомы грамматики | ||
| + | |||
| + | == Определение однозначной КС-грамматики == | ||
| + | КС грамматика называется однозначной или детерминированной, если всякая выводимая терминальная цепочка имеет только одно дерево вывода (соотвественно только один левый и только один правый вывод). | ||
| + | |||
| + | == Определение неоднозначной КС-грамматики == | ||
| + | КС-грамматика G называется неоднозначной, если существует хотя бы одна цепочка α ⊂ L(G), для которой может быть построено два или более различных деревьев вывода. | ||
| + | |||
| + | == Определение недетерминированного МП автомата == | ||
| + | Недетерминированный автомат с магазинной памятью (МП-автомат) — семёрка ''M'' = (''Q'', ''T'', ''Г'', ''D'', ''q''<sub>0</sub>, ''Z''<sub>0</sub>, ''F''), где | ||
| + | # ''Q'' — конечное множество состояний, представляющее всевозможные состояния управляющего устройства | ||
| + | # ''T'' — конечный входной алфавит | ||
| + | # ''Г'' — конечный алфавит магазинных символов | ||
| + | # ''D'' — отображение множества ''Q'' × (''T'' ∪ {ε}) × ''Г'' в множество всех конечных подмножеств ''Q'' × ''Г''*, называемое функцией переходов | ||
| + | # ''q''<sub>0</sub> ∈''Q'' — начальное состояние управляющего устройства | ||
| + | # ''Z''<sub>0</sub> ∈''Г'' — символ, находящийся в магазине в начальный момент (начальный символ магазина) | ||
| + | # ''F'' ⊆''Q'' — множество заключительных состояний | ||
| + | |||
| + | == Определение детерминированного МП автомата == | ||
| + | Детерминированный автомат с магазинной памятью (МП-автомат) — семёрка ''M'' = (''Q'', ''T'', ''Г'', ''D'', ''q''<sub>0</sub>, ''Z''<sub>0</sub>, ''F''), где | ||
| + | # ''Q'' — конечное множество состояний, представляющее всевозможные состояния управляющего устройства | ||
| + | # ''T'' — конечный входной алфавит | ||
| + | # ''Г'' — конечный алфавит магазинных символов | ||
| + | # ''D'' — отображение множества ''Q'' × (''T'' ∪ {ε}) × ''Г'' в множество всех конечных подмножеств ''Q'' × ''Г''*, называемое функцией переходов | ||
| + | # ''q''<sub>0</sub> ∈ ''Q'' — начальное состояние управляющего устройства | ||
| + | # ''Z''<sub>0</sub> ∈ ''Г'' — символ, находящийся в магазине в начальный момент (начальный символ магазина) | ||
| + | # ''F'' ⊆ ''Q'' — множество заключительных состояний | ||
| + | Кроме того, должны выполняться следующие условия: | ||
| + | # Множество ''D''(''q'', ''a'', ''Z'') содержит не более одного элемента для любых ''q'' ∈ ''Q'', ''a'' ∈ ''T'' ∪ {ε}, ''Z''<sub>0</sub> ∈ ''Г'' | ||
| + | # Если ''D''(''q'', ε, ''Z'') ≠ ∅, то ''D''(''q'', ''a'', ''Z'') = ∅ для всех ''a'' ∈ ''T'' | ||
| + | |||
| + | == Определение конфигурации МП автомата == | ||
| + | Конфигурацией автомата с магазинной памятью (МП автомата) называется тройка (''q'', ''w'', ''u''), где | ||
| + | * ''q'' ∈ ''Q'' — текущее состояние магазинного устройства | ||
| + | * ''w'' ∈ ''T''* — непрочитанная часть входной цепочки; первый символ цепочки ''w'' находится под входной головкой; если ''w'' = ε, то считается, что входная лента прочитана | ||
| + | * ''u'' ∈ ''Г''* — содержимое магазина; самый левый символ цепочки ''u'' считается вершиной магазина; если ''u = ε, то магазин считается пустым | ||
| + | |||
| + | == Определение языка, допускаемого МП автоматом == | ||
| + | Цепочка ''w'' допускается МП автоматом, если (''q''<sub>0</sub>, ''w'', ''Z''<sub>0</sub>)⊢* (''q'', ε, ''u'') для некоторых ''q'' ∈ ''F'' и ''u'' ∈ ''Г''*. Язык, допускаемый МП-автоматом ''M'' — множество всех цепочек, допускаемых автоматом ''M''. | ||
| + | |||
| + | == Определение недетерминированного МП автомата, допускающего опустошением магазина == | ||
| + | Цепочка ''w'' допускается МП автоматом, если (''q''<sub>0</sub>, ''w'', ''Z''<sub>0</sub>)⊢* (''q'', ε, ε) для некоторого ''q'' ∈ ''Q''. В таком случае говорят, что автомат допускает цепочку ''опустошением магазина''. | ||
| + | |||
| + | == Соотношение, между языками, порождаемыми КС-грамматиками, и языками, допускаемыми недетерминированными МП автоматами == | ||
| + | Они совпадают. | ||
| + | |||
| + | == Формулировка леммы о разрастании для КС-языков == | ||
| + | Для любого контекстно-свободного языка L существуют такие целые l и k, что любая цепочка α ∈ L, |α| > l представима в виде α = uvwxy, где | ||
| + | # |vwx| <= k | ||
| + | # vx != e | ||
| + | # uv<sup>i</sup>wx<sup>i</sup>y ∈ L для любого i >= 0 | ||
| + | |||
| + | == Определение нормальной формы Хомского для КС-грамматики == | ||
| + | говорят что КС-грамматика находится в нормальной форме Хомского если каждое правило имеет вид: | ||
| + | # Либо A → BC, A,B,C - нетерминалы | ||
| + | # либо A → α, α - терминал | ||
| + | # либо S → e, в таком случае S не встречается в правых частях правил | ||
| + | |||
| + | == Определение правостороннего вывода в КС-грамматике == | ||
| + | Вывод, в котором в любой сентенциальной форме на каждом шаге делается подстановка самого правого нетерминала, называется '''правосторонним'''. | ||
| + | |||
| + | == Определение левостороннего вывода в КС-грамматике == | ||
| + | Вывод, в котором в любой сентенциальной форме на каждом шаге делается подстановка самого левого нетерминала, называется '''левосторонним'''. | ||
| + | |||
| + | == Что такое леворекурсивная грамматика? == | ||
| + | '''Грамматика''' называется '''леворекурсивной''', если в ней имеется нетерминал A такой, что существует вывод A ⇒<sup>+</sup> Au для некоторой строки u. | ||
| + | |||
| + | == Определение множества FIRST1 == | ||
| + | FIRST1 — множество всех терминальных символов, с которых может начинаться цепочка терминальных символов, выводимых из цели грамматики или ε, если u ⇒* ε. | ||
| + | |||
| + | Пример: | ||
| + | |||
| + | * S → aS | A | ||
| + | * A → b | bSd | bA | ε | ||
| + | * FIRST1 = {a, b, ε} | ||
| + | |||
| + | == Определение множества FOLLOW1 == | ||
| + | == Определение LL(1) грамматики == | ||
| + | LL(1)-грамматика - грамматика, для которой таблица предсказывающего анализатора не имеет неоднозначно определенных входов | ||
| + | |||
| + | == Определение LR(1) ситуации == | ||
| + | LR(1)-ситуацией называется пара [''A'' → α . β, ''a''], где ''A'' → α β — правило грамматики, ''a'' — терминал или правый концевой маркер $. Вторая компонента ситуации называется аванцепочкой. | ||
| + | |||
| + | == Определение LR(1) грамматики == | ||
| + | Грамматика называется LR(1), если из условий | ||
| + | |||
| + | 1. <math>S' =>_r uAw =>_r uvw</math>, | ||
| + | |||
| + | 2. <math>S' =>_r zBx =>_r uvy</math>, | ||
| + | |||
| + | 3. FIRST(w) = FIRST(y) | ||
| + | |||
| + | следует, что uAy = zBx (т.е. u = z, A = B и x = y). | ||
| + | |||
| + | == Какого типа конфликты могут появиться в канонической системе множеств LR(1) ситуаций? == | ||
| + | Shift-Reduce и Reduce-Reduce | ||
| + | == Определение конфигурации LR-анализатора == | ||
| + | Пара (Содержимое магазина, непросмотренный вход) | ||
| + | == Как меняется конфигурация LR-анализатора при действии reduce? == | ||
| + | Убрать из стека правую часть правила, добавить левую и состояние goto(последнее состояние в магазине, символ из левой части правила) | ||
| + | == Какие типы действий выполняет LR-анализатор? == | ||
| + | Shift, Reduce, Accept, Reject | ||
| + | == Как меняется конфигурация LR-анализатора при действии shift? == | ||
| + | Перенести верхний символ входа в магазин, занести наверх магазина состояние action(предыдущее состояние, взятый символ) | ||
| + | == Что такое основа правой сентенциальной формы == | ||
| + | |||
| + | Основа правой сентенциальной формы z - это правило вывода <math>A -> v</math> и позиция в z, в которой может быть найдена цепочка v такие, что в результате замены v на A получается предыдущая сентенциальная форма в правостороннем выводе z. Таким образом, если <math>S =>_r avb</math>, то <math>A -> v</math> в позиции, следующей за a - это основа цепочки <math>avb</math>. Подцепочка b справа от основы содержит только терминальные символы. | ||
{{Курс Конструирование Компиляторов}} | {{Курс Конструирование Компиляторов}} | ||
Текущая версия
см. также ответы на вопросы теоретического минимума 2007 года, список определений.
[править] Алфавит
Алфавит - конечное множество символов
[править] Определение грамматики
Грамматика 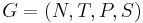 - четверка множеств, где
- четверка множеств, где
-
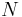 - алфавит нетерминальных символов
- алфавит нетерминальных символов
-
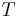 - алфавит терминальных символов,
- алфавит терминальных символов, 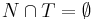 ;
;
-
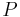 - множество правил вида
- множество правил вида 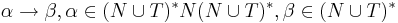
-
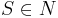 - начальный символ или аксиома грамматики
- начальный символ или аксиома грамматики
[править] Определение грамматик типа 0 по Хомскому
Если на грамматику 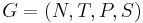 не накладываются никакие ограничения, то её называют грамматикой типа 0, или грамматикой без ограничений.
не накладываются никакие ограничения, то её называют грамматикой типа 0, или грамматикой без ограничений.
[править] Определение грамматик типа 1 (неукорачивающих) по Хомскому
Если
- Каждое правило грамматики, кроме
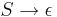 , имеет вид
, имеет вид 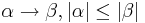
- В том случае, когда
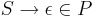 , символ
, символ 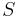 не встречается в правых частях правил
не встречается в правых частях правил
то грамматику называют грамматикой типа 1, или неукорачивающей.
[править] Грамматика типа 2 (Контекстно-свободная, КС) по Хомскому
Грамматика типа 2 (Контекстно-свободная, КС) - грамматика, где каждое правило 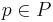 имеет вид
имеет вид 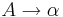 , где
, где 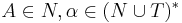
[править] Грамматика типа 3 (Праволинейная) по Хомскому
Грамматика типа 3 (Праволинейная) - грамматика, где 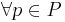 имеет вид либо
имеет вид либо 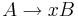 , либо
, либо 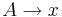 , где
, где 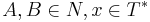
[править] Определение детерминированной машины Тьюринга
Детерминированная машина Тьюринга — Tm = (Q, Г, Σ, D, q0, F)
- Q — конечное множество состояний
- Г — конечное множество ленточных символов (конечный алфавит), один из которых называется пустым и обозначается обычно b
- Σ — входной алфавит, Σ ⊆ Г\{b} (b - пустой символ)
- D — правила перехода
- D: (Q\F) × Г → Q × Г × {L, R}
- q0 ∈ Q — начальное состояние
- F ⊆ Q — множество конечных состояний
[править] Определение конфигурации машины Тьюринга
Конфигурацией машины Тьюринга называется тройка (q, w, i), где
- q ∈ Q — состояние машины Тьюринга
- w ∈ Г* —текущее содержимое занятого участка ленты, w = a1 … an
- i ∈ Z — положение головки машины Тьюринга
[править] Определение языка, допускаемого машиной Тьюринга
Язык, допускаемый машиной Тьюринга — множество таких слов w, что, машина Тьюринга, находясь в состоянии (q0, w, 1) может достигнуть через конечное число переходов состояния q ∈ F.
[править] Соотношение между языками, порождаемыми грамматиками типа 0 и языками, допускаемыми машинами Тьюринга
Класс языков, допускаемых машиной Тьюринга, эквивалентен классу языков, порождаемых грамматиками типа 0.
[править] Объяснить разницу между недетерминированной и детерминированной машиной Тьюринга
Детерминированная машина Тьюринга из данного состояния по данному символу может сделать не более одного перехода, недетерминированная же таким свойством не обладает.
[править] Определение регулярного множества
Регулярное множество в алфавите T определяется следующим образом:
-
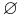 — регулярное множество в алфавите T
— регулярное множество в алфавите T
-
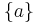 — регулярное множество в алфавите T для каждого a ∈ T
— регулярное множество в алфавите T для каждого a ∈ T
-
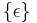 — регулярное множество в алфавите T
— регулярное множество в алфавите T
- Если P и Q — регулярные множества в алфавите T, то регулярны множества
-
 (объединение)
(объединение)
-
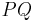 (конкатенация,
(конкатенация, 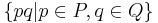 )
)
-
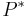 (итерация:
(итерация: 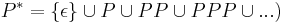
-
- Ничто другое не является регулярным множеством в алфавите T
[править] Определение регулярного выражения
Регулярное выражение — форма записи регулярного множества.
Регулярное выражение и обозначаемое им регулярное множество определяются следующим образом:
- ∅ — обозначает множество {}
- ε — обозначает множество {ε}
- a — обозначает множество {a}
- Если РВ p и q обозначают множества P и Q соответственно, то:
- (p|q) обозначает P ∪ Q
- pq обозначает PQ
- (p*) обозначет P*
- Ничто другое не является регулярным выражением в данном алфавите
[править] Определение праволинейной грамматики
Праволинейная грамматика или грамматика типа 3 по Хомскому — грамматика вида A → w, A → wB, w ∈ T*.
[править] Определение недетерминированного конечного автомата
Недетерминированный конечный автомат - M = (Q, Σ, D, q0, F)
- Q — конечное непустое множество состояний
- Σ — входной алфавит
- D — правила перехода
- Q × ( Σ ∪ {ε} ) → 2Q
- q0 ∈ Q — начальное состояние
- F ⊆ Q — множество конечных состояний
[править] Определение детерминированного конечного автомата
Детерминированный конечный автомат - M = (Q, Σ, D, q0, F)
- Q — конечное непустое множество состояний
- Σ — конечный входной алфавит
- D — правила перехода
- Q × Σ → Q
- q0 ∈ Q — начальное состояние
- F ⊆ Q — множество конечных состояний
[править] Объяснить разницу между недетерминированным и детерминированным конечным автоматом
Недетерминированный конечный автомат является обобщением детерминированного. Существует теорема, гласящая, что «Любой недетерминированный конечный автомат может быть преобразован в детерминированный так, чтобы их языки совпадали» (такие автоматы называются эквивалентными). В детерменированном автомате из одного состояния допускается не более одного перехода для каждого символа алфавита, в недетерменированном - произвольное количество. Кроме того, в НКА возможны эпсилон-переходы.
[править] Определение конфигурации конечного автомата
Пусть M = (Q, T, D, q0, F) — НКА. Конфигурацией автомата M называется пара (q, ω) ∈ Q × T*, где q — текущее состояние управляющего устройства, а ω — цепочка символов на входной ленте, состоящая из символов под головкой и всех символов справа от неё.
[править] Определение языка, допускаемого конечным автоматом
Автомат M допускает цепочку ω, если (q0, ω) ⊦* (q, ε) для некоторого q ∈ F. Языком, допускаемым автоматом M, называется множество входных цепочек,допускаемых автоматом M. То есть:
- L(M) = {ω | ω ∈ T* и (q0, ω) ⊦* (q, ε) для некоторого q ∈ F}
[править] Определение ε-замыкания для подмножества состояний НКА
ε-замыкание множества состояний R, R ⊆ Q — множество состояний НКА, достижимых из состояний, входящих в R, посредством только переходов по ε, то есть множество
- S = ⋃q ∈ R {p | (q, ε) ⊦* (p, ε)}
[править] Определение расширенной функции переходов для КА
Расширенная функция переходов множества состояний R, R ⊆ Q по a — множество состояний НКА, в которые есть переход на входе a для состояний из R, то есть множество
- S = ⋃q ∈ R {p | p ∈ D(q, a)}
[править] Определение расширенной функции переходов для НКА
[править] Определение расширенной функции переходов для ДКА
[править] Определение функции firstpos для поддерева в дереве регулярного выражения
Функция firstpos(n) для каждого узла n узла синтаксического дерева регулярных выражений даёт множество позиций, которые соответствуют первым символам в цепочках, генерируемых подвыражением с вершиной n. Построение:
| узел n | firstpos(n) |
|---|---|
| ε | ∅ |
| i ≠ ε | {i} |
| u | v | firstpos(u) ∪ firstpos(v) |
| u . v | if nullable(u) then firstpos(u) ∪ firstpos(v) else firstpos(u) |
| v* | firstpos(v) |
[править] Определение функции lastpos для поддерева в дереве регулярного выражения
Функция lastpos(n) для каждого узла n узла синтаксического дерева регулярных выражений даёт множество позиций, которым соответствуют последние символы в цепочках, генерируемых подвыражениями с вершиной n. Построение lastpos(n):
| узел n | lastpos(n) |
|---|---|
| ε | ∅ |
| i ≠ ε | {i} |
| u | v | lastpos(u) ∪ lastpos(v) |
| u . v | if nullable(v) then lastpos(u) ∪ lastpos(v) else lastpos(v) |
| v* | lastpos(v) |
[править] Определение функции followpos для позиций в дереве регулярного выражения
Функция followpos(i) для позиции i есть множество позиций j таких, что существует некоторая строка …cd…, входящая в язык, описываемый регулярным выражением, такая, что позиция i соответствует вхождению c, а позиция j — вхождению d.
[править] Сформулировать соотношение между регулярными множествами и языками, допускаемыми КА
Любой конечный автомат распознает регулярное множество цепочек символов входного алфавита. Верно и обратное — для любого регулярного языка можно построить распознающий его конечный автомат.
[править] Определение регулярной грамматики
Регулярные грамматики — праволинейные (A → w, A → wB, w ∈ T*), леволинейные (A → w, A → Bw, w ∈ T*).
[править] Сформулировать соотношение между языками, порождаемыми праволинейными грамматиками и языками, допускаемыми КА
Для любой праволинейной грамматики существует конечный автомат, проверяющий порождаемый грамматикой язык. Для любого конечного автомата существует праволинейная грамматика, порождающая проверяемый конечным автоматом язык.
[править] Определение эквивалентных состояний ДКА
Два состояния qi и qj называются эквивалентными (qi ~ qj), если 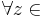 T* верно, что
T* верно, что 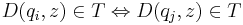
[править] Определение различимых состояний ДКА
[править] Определение контекстно-свободной грамматики без ε-правил
- A → α, α ∈ (N ∪ T)+
- допускается S → ε, если S не входит ни в какую правую часть
[править] Определение контекстно-свободной грамматики
A → α, α ∈ (N ∪ T)*
[править] Определение выводимости в грамматике
Определим на множестве (N ∪ T)* грамматики G = (N, T, P, S) бинарное отношение выводимости «⇒» следующим образом: если δ → γ ∈ P, то αδβ ⇒ αγβ для всех α, β ∈ (N ∪ T)*. Если α1 ⇒ α2, то α2 непосредственно выводима из α1.
Если α ⇒k β (k ≥ 0), то существует последовательность шагов
- γ0 ⇒ γ1 ⇒ γ2 ⇒ … ⇒ γk − 1 ⇒ γk
где α = γ0 и β = γk. Последовательность цепочек γ0, γ1, γ2, …, γk − 1, γk в этом случае называется выводом β из α.
[править] Определение языка, порождаемого КС-грамматикой
Языком, порождаемым грамматикой G = (N, T, P, S) (обозначается L(G)) называется множество всех цепочек терминалов, выводимых из аксиомы, то есть:
- L(G) = {w | w ∈ T*, S ⇒+ w}
[править] Определение сентенциальной формы
Сентенциальная форма — цепочка над алфавитом 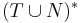 , выводимая из аксиомы грамматики
, выводимая из аксиомы грамматики
[править] Определение однозначной КС-грамматики
КС грамматика называется однозначной или детерминированной, если всякая выводимая терминальная цепочка имеет только одно дерево вывода (соотвественно только один левый и только один правый вывод).
[править] Определение неоднозначной КС-грамматики
КС-грамматика G называется неоднозначной, если существует хотя бы одна цепочка α ⊂ L(G), для которой может быть построено два или более различных деревьев вывода.
[править] Определение недетерминированного МП автомата
Недетерминированный автомат с магазинной памятью (МП-автомат) — семёрка M = (Q, T, Г, D, q0, Z0, F), где
- Q — конечное множество состояний, представляющее всевозможные состояния управляющего устройства
- T — конечный входной алфавит
- Г — конечный алфавит магазинных символов
- D — отображение множества Q × (T ∪ {ε}) × Г в множество всех конечных подмножеств Q × Г*, называемое функцией переходов
- q0 ∈Q — начальное состояние управляющего устройства
- Z0 ∈Г — символ, находящийся в магазине в начальный момент (начальный символ магазина)
- F ⊆Q — множество заключительных состояний
[править] Определение детерминированного МП автомата
Детерминированный автомат с магазинной памятью (МП-автомат) — семёрка M = (Q, T, Г, D, q0, Z0, F), где
- Q — конечное множество состояний, представляющее всевозможные состояния управляющего устройства
- T — конечный входной алфавит
- Г — конечный алфавит магазинных символов
- D — отображение множества Q × (T ∪ {ε}) × Г в множество всех конечных подмножеств Q × Г*, называемое функцией переходов
- q0 ∈ Q — начальное состояние управляющего устройства
- Z0 ∈ Г — символ, находящийся в магазине в начальный момент (начальный символ магазина)
- F ⊆ Q — множество заключительных состояний
Кроме того, должны выполняться следующие условия:
- Множество D(q, a, Z) содержит не более одного элемента для любых q ∈ Q, a ∈ T ∪ {ε}, Z0 ∈ Г
- Если D(q, ε, Z) ≠ ∅, то D(q, a, Z) = ∅ для всех a ∈ T
[править] Определение конфигурации МП автомата
Конфигурацией автомата с магазинной памятью (МП автомата) называется тройка (q, w, u), где
- q ∈ Q — текущее состояние магазинного устройства
- w ∈ T* — непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой; если w = ε, то считается, что входная лента прочитана
- u ∈ Г* — содержимое магазина; самый левый символ цепочки u считается вершиной магазина; если u = ε, то магазин считается пустым
[править] Определение языка, допускаемого МП автоматом
Цепочка w допускается МП автоматом, если (q0, w, Z0)⊢* (q, ε, u) для некоторых q ∈ F и u ∈ Г*. Язык, допускаемый МП-автоматом M — множество всех цепочек, допускаемых автоматом M.
[править] Определение недетерминированного МП автомата, допускающего опустошением магазина
Цепочка w допускается МП автоматом, если (q0, w, Z0)⊢* (q, ε, ε) для некоторого q ∈ Q. В таком случае говорят, что автомат допускает цепочку опустошением магазина.
[править] Соотношение, между языками, порождаемыми КС-грамматиками, и языками, допускаемыми недетерминированными МП автоматами
Они совпадают.
[править] Формулировка леммы о разрастании для КС-языков
Для любого контекстно-свободного языка L существуют такие целые l и k, что любая цепочка α ∈ L, |α| > l представима в виде α = uvwxy, где
- |vwx| <= k
- vx != e
- uviwxiy ∈ L для любого i >= 0
[править] Определение нормальной формы Хомского для КС-грамматики
говорят что КС-грамматика находится в нормальной форме Хомского если каждое правило имеет вид:
- Либо A → BC, A,B,C - нетерминалы
- либо A → α, α - терминал
- либо S → e, в таком случае S не встречается в правых частях правил
[править] Определение правостороннего вывода в КС-грамматике
Вывод, в котором в любой сентенциальной форме на каждом шаге делается подстановка самого правого нетерминала, называется правосторонним.
[править] Определение левостороннего вывода в КС-грамматике
Вывод, в котором в любой сентенциальной форме на каждом шаге делается подстановка самого левого нетерминала, называется левосторонним.
[править] Что такое леворекурсивная грамматика?
Грамматика называется леворекурсивной, если в ней имеется нетерминал A такой, что существует вывод A ⇒+ Au для некоторой строки u.
[править] Определение множества FIRST1
FIRST1 — множество всех терминальных символов, с которых может начинаться цепочка терминальных символов, выводимых из цели грамматики или ε, если u ⇒* ε.
Пример:
* S → aS | A
* A → b | bSd | bA | ε
* FIRST1 = {a, b, ε}
[править] Определение множества FOLLOW1
[править] Определение LL(1) грамматики
LL(1)-грамматика - грамматика, для которой таблица предсказывающего анализатора не имеет неоднозначно определенных входов
[править] Определение LR(1) ситуации
LR(1)-ситуацией называется пара [A → α . β, a], где A → α β — правило грамматики, a — терминал или правый концевой маркер $. Вторая компонента ситуации называется аванцепочкой.
[править] Определение LR(1) грамматики
Грамматика называется LR(1), если из условий
1. S' = > ruAw = > ruvw,
2. S' = > rzBx = > ruvy,
3. FIRST(w) = FIRST(y)
следует, что uAy = zBx (т.е. u = z, A = B и x = y).
[править] Какого типа конфликты могут появиться в канонической системе множеств LR(1) ситуаций?
Shift-Reduce и Reduce-Reduce
[править] Определение конфигурации LR-анализатора
Пара (Содержимое магазина, непросмотренный вход)
[править] Как меняется конфигурация LR-анализатора при действии reduce?
Убрать из стека правую часть правила, добавить левую и состояние goto(последнее состояние в магазине, символ из левой части правила)
[править] Какие типы действий выполняет LR-анализатор?
Shift, Reduce, Accept, Reject
[править] Как меняется конфигурация LR-анализатора при действии shift?
Перенести верхний символ входа в магазин, занести наверх магазина состояние action(предыдущее состояние, взятый символ)
[править] Что такое основа правой сентенциальной формы
Основа правой сентенциальной формы z - это правило вывода A − > v и позиция в z, в которой может быть найдена цепочка v такие, что в результате замены v на A получается предыдущая сентенциальная форма в правостороннем выводе z. Таким образом, если S = > ravb, то A − > v в позиции, следующей за a - это основа цепочки avb. Подцепочка b справа от основы содержит только терминальные символы.


