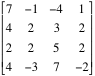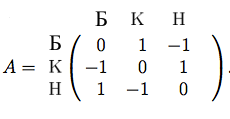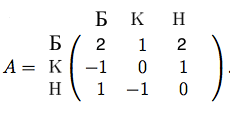Тигры, контрольная 1

Материал из eSyr's wiki.

Версия 02:37, 7 октября 2012

Описание

В 2012 году лектор дал всего две задачи. В обеих был параметр N, который на самом деле мало на что влиял. Его надо было посчитать как количество букв вашего ФИО, то есть для Потапенко Виктор Алексеевич параметр N = 25. Оценка складывалась из 2 за присутствие и по 1,5 за каждую из задач (за каждый из трех подпунктов первой задачи по 0,5). При неправильно посчитанном N лектор ставил 2. В проходе аудитории (П8) стоял стол, который мешал ходить, и, возможно поэтому, лектор не ходил и не проверял валидность конспектов, отсутствие телефонов и пр. На все давалось примерно 20 минут

Теория

Седловые точки

Седловая точка матрицы - это формально такой элемент матрицы, что в своем столбце он самый большой (один из самых больших, т.е. не строго >), а в своей строке он один из самых маленьких. Например в матрице

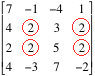
седловая точка - это элемент в первом столбце второй строке, так как он >= всех остальных элементов первого столбца и <= всех остальных элементов второй строки. Довольно просто показать, что если у матрицы несколько седловых точек, то все их значения равны. Для поиска всех седловых точек в матрицах большой размерности не нужно рассматривать каждый элемент отдельно, можно воспользоваться алгоритмом, опирающимся на вспомогательную теорему. Работу алгоритма покажем на примере поиска всех седловых точек матрицы

Соберем наименьшие значения по всем строкам, получим (-4, 2, 2, -3). Также соберем наибольшие значения по всем столбцам (7, 2, 7, 2). Проверим, равно ли наибольшее из чисел первого набора наименьшему числу из второго набора. В нашем случае это так и это число 2. Если бы оказалось, что максимум первого набора меньше, чем минимум второго, то седловых точек не было бы. А ситуации, что максимум первого набора больше минимума второго вообще быть не может, доказывается отдельно. Итак, теперь посмотрим, на каких позициях стоят 2-ки в наших наборах. В первом это {2, 3}, а во втором это {2, 4}. На произведении этих множеств и располагаются все седловые точки (то есть {2, 3} X {2, 4} = { {2, 2}, {3, 2}, {2, 4}, {3, 4} } )

Но причем здесь теория игр? Дело в том что при игре один-на-один, когда интересы игроков прямо противоположны мы пользуемся матрицами стратегий и понятием седловых точек. Например при игре в "камень ножницы бумага" матрица стратегий выглядит так

где стратегия - это непосредственно выбор камня, ножниц или бумаги, а на пересечениях стратегий выигрыш первого игрока. первый игрок выбирает строку, второй выбирает столбец. Можно проверить, что у этой матрицы нет седловых точек. Как и почти у всех матриц интересных игр один-на-один. Но представим, что матрица будет выглядеть немного по другому

И на пересечениях стратегий размер выигрыша первого игрока в рублях. То есть, если первый игрок выбрал бумагу и второй игрок выбрал бумагу, то второй платит первому 2 рубля. А если первый игрок выбрал ножницы, а второй камень, то первый игрок платит второму 1 рубль. Понятно, что первый игрок сразу же поймет, что надо все время показывать бумагу, так как тогда он будет только выигрывать. А второй, стараясь проиграть меньше, будет показывать камень, так как показав камень, он проиграет рубль, а не два. Как вы наверное уже догадались, точка в первой строке втором столбце - седловая (можете проверить). Игроки в погоне за выгодой будут выбирать стратегии так, что на их пересечении будут находиться седловые точки. А значение в этой точке (в данном случае 1) называется значением игры. Тройка {оптимальная стратегия Игрока 1, оптимальная стратегия Игрока 2, значение игры} называется решением игры. В нашем случае это {1, 2, 1} (или {Б, К, 1} что тоже самое).

Но мы довольно сильно исказили матрицу стратегий, а значит и правила, игры "камень ножницы бумага". Редкий человек захочет участвовать в ней в роли Игрока 2. Наши коррективы сделали игру несправедливой. Наличие седловой точки, как правило, свидетельствует о несправедливости игры

Смешанные стратегии

Когда седловых точек нет, начинается поиск вероятностей, с которыми надо распределить стратегии, чтобы обеспечить наибольший выигрыш. То есть уже понятно, что нет "волшебной" стратегии, подходящей на все случаи жизни, и что надо выбирать разные стратегии с разными вероятностями

Методы решения матричных игр

Графический алгоритм показан на примере решения второй задачи из контрольной.

Также существует способ выкидывать неинформативные строки и столбцы из матрицы стратегий. Для этого нам нужно понятия слабого доминирования и выпуклой комбинации:

• Вектор a слабо доминирует вектор b, если любой i-ый элемент а больше или равен i-му элементу b.

• Выпуклой комбинацией называет линейную комбинацию векторов, в которой коэффициенты неотрицательны и в сумме дают единицу. Например 0.2a + 0.3b + 0.5c это выпуклая комбинация векторов a, b и c

Итак, строку мы можем выкинуть, если существует выпуклая комбинация остальных строк, слабо доминирующая эту строку. А столбец мы можем выкинуть, только если он слабо доминирует какую-нибудь выпуклую комбинацию остальных столбцов.

Задачи

Задача 1

Пункт а

Ответить на вопрос и обосновать, может ли у матрицы NxN быть ровно (округлено вверх) седловых точек?

Решение

• Для четного N да, так как 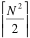это ровно половина элементов матрицы. Так что заполним левую половину нулями, а правую единицами. Получим точно нужное количество элементов, так как все нули у нас - наибольшие в столбцах и наименьшие в строках

• Для нечетного N нет, так как метод нахождения седловых точек, описанный в разделе Теория, основан на теореме, следствием из которой является то, что множество седловых точек представляется как прямоугольник, то есть множество точек [x,y] где x принадлежит X, а y принадлежит Y. То есть количество седловых точек должно раскладываться на два множителя, оба из которых меньше или равны N. Таким образом, у матрицы 3x3 не может быть 7 седловых точек, так как 7 - простое число. А для N =25 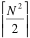=313, а это число не делится нацело ни на одно из чисел от 2 до 25

Пункт б

Ответить на вопрос и обосновать, может ли у матрицы NxN не быть седловых точек?

Решение

Да, конечно. И это даже не зависит от N (при N > 1). Пример

Любой 0 является наименьшим в своей строке, но не является наибольшим в своем столбце.

Любая 1 является наибольшей в своем столбце, но не является наименьшей в своей строке.

Пункт в

Ответить на вопрос и обосновать, может ли у матрицы NxN быть ровно одна седловая точка?

Решение

Да, конечно. И это даже не зависит от N. Пример

Единственная седловая точка здесь это 1 (легко проверить)

Задача 2

Найти решение игры для матрицы стратегий

Будем решать для N = 25, но на самом деле здесь мало что зависит от N. Мы видим, что здесь нет седловых точек, а значит решение существует (причем обязательно) только в смешанных стратегиях

Воспользуемся графическим методом, который рассчитан на матрицы 2xn и mx2

Используя коэффициенты из трех столбцов нашей матрицы, запишем три уравнения прямых

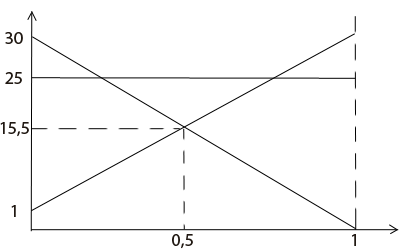
Вычислив точки пересечения, построим графики (p принимает значения от 0 до 1)

Из всех пересечений выбираем те, под которыми не проходят другие прямые, и из них выбираем то, что левее. В нашем случае все просто, это пересечение прямых l1 и l3. Значение p в этой точке 1/2, а значит распределение стратегий первого игрока у нас P = {p, 1-p} = {1/2, 1/2}. Значение игры у нас 15,5 (значение l1 или l3 в точке пересечения). Осталось найти распределение стратегий второго игрока. Для этого нам надо решить еще одно уравнение. У нас пересеклись прямые l1 и l2, поэтому возьмем первый и третий столбец исходной матрицы. В каждом из них из верхнего элемента вычтем нижний (так мы получаем коэффициенты для уравнения второго игрока): k1 = 1 - 30 = -29, k3 = 30 - 1 = 29. Подставим их в уравнение

теперь Q= {q, 0, 1 -q} (для прямых, не участвовавших в пересечении проставляем нулевую вероятность), следовательно Q = {1/2, 0, 1/2}

Ответ: P = {1/2, 1/2}, Q = {1/2, 0, 1/2}, v = 15,5